SOLUTION: * Find the solution to this system of equations, algebraically and graphically. {{{system(x^2-2y^2=16, x^2+4y^2=16)}}} * Graph the solution set of this system of inequalities:

First we draw the graph of the hyperbola



We put it in standard form by getting a 1 on the right
by dividing every term by 16:



Then we find the semi-transverse and semi-conjugate axes 
and draw the defining rectangle, draw the asymptotes and 
sketch the hyperbola:



We do the same with the ellipse   x^2+4y^2=16:



Then we find the semi-major and semi-minor axes and sketch 
the hyperbola:

That gives us this graph (in green).  I'll erase the 
guidelines for the hyperbola and just leave the hyperbola
only:



So we see that the only points the red hyperbola and the green
ellipse have in common are the points

(x,y) = (4,0) and (x,y) = (-4,0)

So when we do the problem algebraically we should get the
values of x as 4 and -4 and the value of y as 0.



Solve the first equation for :

.  Substitute 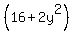 for 
in the second:








Substitute 0 for y in






±.

So we do get for the solutions the same
values algebraically as we saw that the points 
which the hyperbola and the ellipse had in common
graphically. 

(x,y) = (±4,0) or the points: 

(x,y) = (4,0) and (x,y) = (-4,0)        

----------------------------------

Notice that the first is just like the equation for the green
ellipse in the preceding problem except that it has
an  symbol instead of an equal sign .

That is the region on and inside the green ellipse with the
equation .  We draw the ellipse solid 
not dotted because the inequality is  and not 
, and thus the ellipse itself is included in the
graph:



Next we see the inequality 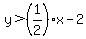.  We draw the
boundary line dotted since the inequality is 
and not  and therefore the graph is only
the area above the line and does not include the line.



So I will erase all the part that is not to be shaded and we have
just the inside area. I can't shade on here, but you can on your 
paper.  



Edwin