|
Question 294406: what is the equation of a hyperbola with vertices (-5,3) (-1,3) and foci (-3-2sqrt(5), 3) and -3-2sqrt(5), 3)
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! what is the equation of a hyperbola with vertices (-5,3) (-1,3) and foci (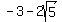 , 3) and ( , 3) and (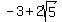 , 3) , 3)
First we plot the vertices:
 We see that the hyperbola opens right and left, that is,
it looks something like this: )(
So we know its standard equation is this:
We see that the hyperbola opens right and left, that is,
it looks something like this: )(
So we know its standard equation is this:
 We connect them to find the transverse axis:
We connect them to find the transverse axis:
 We can see that the transverse axis is 4 units long, and since the
transverse axis is
We can see that the transverse axis is 4 units long, and since the
transverse axis is  units long, then units long, then  and and  The center of the hyperbola is the midpoint of the transverse axis,
and we can see that the midpoint of the transverse axis is (-3,3), so
we have (h,k) = (-3,3) and that a=2.
We are given the foci
foci (
The center of the hyperbola is the midpoint of the transverse axis,
and we can see that the midpoint of the transverse axis is (-3,3), so
we have (h,k) = (-3,3) and that a=2.
We are given the foci
foci (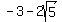 ,3) and ( ,3) and (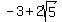 , 3)
We plot the vertex and those two given foci: , 3)
We plot the vertex and those two given foci:
 The number of units from each of the foci to the center is the value c.
To find that distance we can subtract the x-coordinate of the center
from the x-coordinate of the right focus, and get
The number of units from each of the foci to the center is the value c.
To find that distance we can subtract the x-coordinate of the center
from the x-coordinate of the right focus, and get
 Next we find b from the Pythagorean relationship common to all
hyperbolas, which is
Next we find b from the Pythagorean relationship common to all
hyperbolas, which is
 Substituting for c and a
Substituting for c and a




 Next we draw in the conjugate axis which is 2b units
or 8 units long with the center at its midpoint. That is,
we draw a vertical line 4 units upward and 4 units downward
from the center:
Next we draw in the conjugate axis which is 2b units
or 8 units long with the center at its midpoint. That is,
we draw a vertical line 4 units upward and 4 units downward
from the center:
 Next we draw the defining rectangle which has the transverse axis and
the conjugate asis as perpendicular bisectors of its sides:
Next we draw the defining rectangle which has the transverse axis and
the conjugate asis as perpendicular bisectors of its sides:
 Next we draw the extended diagonals of the defining rectangle, which
are the asymptotes of the hyperbola:
Next we draw the extended diagonals of the defining rectangle, which
are the asymptotes of the hyperbola:
 Finally we can sketch in the hyperbola:
Finally we can sketch in the hyperbola:
 But you only wanted the equation. I could have answered that when we
found b, but you will probably have to graph other hyperbolas, so I
thought I would go ahead and complete the graph before giving the equation,
which is gotten by substituting (h,k) = (-3,3), a=2, and b=4 in
But you only wanted the equation. I could have answered that when we
found b, but you will probably have to graph other hyperbolas, so I
thought I would go ahead and complete the graph before giving the equation,
which is gotten by substituting (h,k) = (-3,3), a=2, and b=4 in


 Edwin
Edwin
|
|
|
| |