find the length of the major axis of the ellipse with equation
 We must get that in standard form, which is:
We must get that in standard form, which is:
 if the ellipse looks like this:
if the ellipse looks like this:  ,
or
,
or  if the ellipse looks like this:
if the ellipse looks like this:  ,
Where the length of the major axis is
,
Where the length of the major axis is  and the length of
the minor axis is
and the length of
the minor axis is 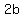 .
.
 All the completing of the square and factoring has already been done, so
we can start by getting a 1 on the right. To do that, we divide through
by 36:
All the completing of the square and factoring has already been done, so
we can start by getting a 1 on the right. To do that, we divide through
by 36:
 Simplifying,
Simplifying,
 Since 9 is greater than 4 it is of the form:
Since 9 is greater than 4 it is of the form:
 so the ellipse looks like this:
so the ellipse looks like this:  ,
Therefore
,
Therefore  and
and  .
The major axis is
.
The major axis is  or
or  or
or  Here is the graph. The ellipse's center is at (-4,1).
Its major axis is the green line which we see is 6 units long.
Here is the graph. The ellipse's center is at (-4,1).
Its major axis is the green line which we see is 6 units long.
 Edwin
Edwin