SOLUTION: I am suppose to graph this conic section how do I do this equation (x+2)=4(y-1)^2

You must learn all the various forms for 
all the various conic sections, and all their
properties.

This one can be placed in standard form:



which is a parabola with a horizontal axis of
symmetry with vertex = (h,k),
distance from vertex to focus and directrix = |p|
which opens right if p is positive and left if p is negative.

Now we put your equation in standard form:



Swap sides:



Multiply both sides by 



Compare to the general standard form:



and we have , , 

So the vertex is (h,k) = (-2,1) and 

and since p is positive the parabola opens to
the right.

So we plot the vertex (-2,1)



and the axis of symmetry is the horizontal line through the vertex,
whose equation is 



We'll draw it in blue:



Since , and since it is positive, the focus
is  of a unit to the right of the vertex, or the point
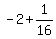(,1) = (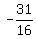,1) = (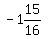,1)

So we plot the focus, but unfortunately, it's so close 
to the vertex, it's hard to plot it so it doesn't run 
into the vertex.



Now we draw the directrix which is a vertical line  of a unit to the left of the vertex.  Its equation is 

 

We'll draw it in green:



Next we draw a horizontal line from the focus directly through
the vertex to the directrix. Unfortunately you can hardly see it 
because it's so short because those points are so close together:


  
Draw a square on each side of that line.  They too are unfortunately
very tiny in this problem:


 
Now we can find the y-intercepts by letting x = 0 in the
original equation and solving for y





±

This gives the y-intercepts at about (0,1.7) and (0.3)

So we plot those:



Finally we draw the parabola through the right corners of the
squares, through the vertex and through the y-intercepts:



That's it.  It's too bad the parabola you picked to plot had 
such a tiny value of p.

Edwin