|
Question 202383: Can anyone help me with ANY of these problems? Please!
1) Solve the following system.
x^2 + y^2 = 25
2x + y = 10
The solution set {(___,___),(___,___)}
2) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). Using k for the constant of proportionality, express the relationship between V and l if V varies directly with l.
V = _______
3) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). If one of the boxes has a volume of 325 cubic inches and a length of 13 inches, what is the constant of proportionality for the group of boxes?
k = ________
4) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). If a box in the group has a length of 25 inches and k = 15, what is its volume?
_____ cubic inches
5) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). If a box in the group has a length of 30 inches, and the girth of 20 inches (perimeter of the side formed by the width and height), what is its height? Use k = 24. (Hint: Volume = length * width * height. Solve for length, and substitute into the equation for constant of proportionality.)
____ inches or ____ inches
Thanks for all your help,
~Sarah
Found 2 solutions by stanbon, jsmallt9:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) Solve the following system.
x^2 + y^2 = 25
2x + y = 10
-----------
Solve the 2nd equation for "y":
y = 10-2x
--
Substitute that into the 1st equation and solve for "x":
x^2 + (10-2x)^2 = 25
x^2 + 100 - 40x + 4x^2 = 25
5x^2 - 40x + 75 = 0
x^2 - 8x + 15 = 0
x^2-5x-3x+15 = 0
x(x-5) -3(x-5) = 0
(x-5)(x-3) = 0
x = 3 or x = 5
------------------------
y=10-2x
If x = 3, then y = 10 - 6 = 4
If x = 5, then y = 10 -10 = 0
The solution set {(3,4),(5,0)}
===============================================
2) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l).
Using k for the constant of proportionality, express the relationship between V and l if V varies directly with l.
V = kl
=================================================
3) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l).
V = kl
If one of the boxes has a volume of 325 cubic inches and a length of 13 inches, what is the constant of proportionality for the group of boxes?
k = 325/13 = 25
==================================================
4) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). If a box in the group has a length of 25 inches and k = 15, what is its volume?
V=kl
V=15*25
= 375 cubic inches
==================================================
5) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). If a box in the group has a length of 30 inches, and the girth of 20 inches (perimeter of the side formed by the width and height), what is its height? Use k = 24. (Hint: Volume = length * width * height. Solve for length, and substitute into the equation for constant of proportionality.)
---
V=kl
l = V/k
30 =V/24
V = 720 cu. in.
height = V/[length*width]
height = V/[30*width)
Comment: width seems to be unknown
__?__ inches or __?__ inches
=========================================
Cheers,
Stan H.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) Solve the following system.
x^2 + y^2 = 25
2x + y = 10
Probably the simplest way to solve this system is to take the linear equation, the second one, solve it for one of the variables, substitute for that variable into the non-linear equation (the first one) and then solve that:
Adding -2x to both sides of the second equation we get
y = -2x + 10
Substituting for y in the first equation, remembering that it is always a good idea to surround the expression be parentheses, we get:

To solve this we will need to simplify it and then use one the techniques of solving a quadratic equation. To simplify 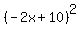 we can either use the binomial square formula (if we remember it): we can either use the binomial square formula (if we remember it):  or actually multiply out (-2x + 10)(-2x + 10). Either way we get: or actually multiply out (-2x + 10)(-2x + 10). Either way we get:

Adding like terms:

Since the two easier techniques for solving quadratic equations require one side to be zero, we'll -25 to both sides:

Now we can either use the quadratic formula or try to factor the left side. Factoring the Greatest Common Factor (GCF) out we get:

Then the trinomial factors:

Since the only way for a product to be zero at least one of the factors must be zero:
x-3 = 0 or x-5 = 0
Solving each of these we get
x = 3 or x = 5
One at a time we will substitute these x-values into one of the original equations. (The second one is easier.)
2(3) + y = 10
which gives y = 4. And
2(5) + y = 10
which gives y = 0
So there are two solutions:
(3, 4) and (5, 0)
2) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). Using k for the constant of proportionality, express the relationship between V and l if V varies directly with l.
When it says that the volume "varies directly" with the length, it means that the volume is equal to some number, called the constant of proportionality, times the length. Since the problem says to use "k" for the constant of proportionality, the equation becomes:
V = k*l
(We will use this equation of #3, #4 and #5.)
3) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). If one of the boxes has a volume of 325 cubic inches and a length of 13 inches, what is the constant of proportionality for the group of boxes?
Our equation, V = k*l has three unknowns: V, k and l. This problem gives us numbers to use for two of them: V and l. We should then be able to use the equation to solve for the third: k
325 = k*(13)
Dividing both sides by 13 we get:
25 = k
4) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). If a box in the group has a length of 25 inches and k = 15, what is its volume?
This time we are given "l" and "k" and we are looking for V:
V = (15)*(25) = 375
5) Complete the following item based on the given information.
The volume of a box(V) varies directly with its length(l). If a box in the group has a length of 30 inches, and the girth of 20 inches (perimeter of the side formed by the width and height), what is its height? Use k = 24. (Hint: Volume = length * width * height. Solve for length, and substitute into the equation for constant of proportionality.)
This time we are asked to find something, height, which is not even in our formula from #2. But we are given another formula for volume and information about the girth, both of which include the height.
To start with:- Remember that there are often many ways to solve a Math problem.
- The second part of the hint, "Solve for length..." does not help as far as I can see. I think it should say ("Solve for height..." or "Solve for width...".
My solution is based on recognizing that the volume of the box will be the same whether V = k*l or V = l*w*h is used to calculate it. So the right sides of these equations must be equal:
k*l = l*w*h
Dividing both sides of this by "l" we have:
k = w*h
Replacing k with its value, 24, we get:
24 = w*h
We now have an equation with two variables. We need another equation with the same two variables in order to solve the problem. The second equation comes from the girth information.
We are told that the girth, a rectangle formed by the width and height, is 20. With the formula for perimeter of a rectangle (or by just adding the four sides) we should get:
2w + 2h = 20
Now we have a system, a little like #1, which we can solve: Solve the linear equation (second) for either of the variables and then substitute into the non-linear (first) equation. Solving the second equation for h...
Add -2w to both sides:
2h = -2w + 20
Divide both sides by 2 (or multiply both sides by 1/2):
h = -w + 10
Now we substitute for h in the first equation:
24 = w*(-w + 10)
Solving this we start by simplifying:

Adding  and and 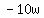 to both sides: to both sides:

Factoring we get:
(w - 4)(w - 6) = 0
Finding the value of w that make the factors zero we get:
w = 4 or w = 6
Substituting these w-values back into the second equation so we can find h, we get:
h = 6 when w = 4 or h = 4 when w = 6. So we have two solutions: The height is 6 and the width is 4 or the height is 4 and the width is 6. (NOTE: At no point did we need to know what the length is (as long it it was not zero). In fact, the length could be any number (except zero) and the widths and heights would still be 4 and 6!)
|
|
|
| |