What is the graph of the equation x2 + y2 - 8x + 6y + 24 = 0
This is a circle because  and
and  have the
have the
same coefficient when on the same side of the equation.

We must first get the equation in standard form:
 Rearrange to get the x terms together and the y terms togethsr.
That is, swap the middle two terms:
Rearrange to get the x terms together and the y terms togethsr.
That is, swap the middle two terms:

 Out to the side or on scratch paper,
we complete the square of
Out to the side or on scratch paper,
we complete the square of
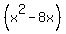 :
1. Multiply the coefficient, -8, of
:
1. Multiply the coefficient, -8, of  , by
, by  ,
getting
,
getting  .
2. Then square
.
2. Then square  , getting +16
3. Add +16 to the left side inside the first parentheses, and
also add it to the right side:
, getting +16
3. Add +16 to the left side inside the first parentheses, and
also add it to the right side:
 Now we complete the square of
Now we complete the square of
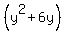 :
1. Multiply the coefficient, 6, of
:
1. Multiply the coefficient, 6, of  , by
, by  ,
getting
,
getting  .
2. Then square
.
2. Then square  , getting +9
3. Add +9 to the left side inside the first parentheses, and
also add it to the right side:
, getting +9
3. Add +9 to the left side inside the first parentheses, and
also add it to the right side:
 Factor each parentheses:
Factor each parentheses:
 Write as perfect squares:
Write as perfect squares:
 Add -24 to both sides:
Add -24 to both sides:
 Compare to the standard form:
Compare to the standard form:
 This has center (h,k) and radius r.
This has center (h,k) and radius r.
 so
so  ,
,  , so
, so  .
.  , so
, so  so the center, (h,k) = (4,-3) and the radius is 1.
So we plot the center (4,-3).
so the center, (h,k) = (4,-3) and the radius is 1.
So we plot the center (4,-3).
 Get a compass and open it one unit wide. Place the sharp
point of the compass on the center and draw the circle.
That is the graph:
Get a compass and open it one unit wide. Place the sharp
point of the compass on the center and draw the circle.
That is the graph:
 Edwin
Edwin