|
Question 134123This question is from textbook Merill Algebra 2 with Trigonometry Aplications and Connections
: i dont understand how to complete the square on y=.5x^2-3x+19/2. i also have to graph this parabola and i dont know how
This question is from textbook Merill Algebra 2 with Trigonometry Aplications and Connections
Found 2 solutions by ankor@dixie-net.com, josmiceli:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! i dont understand how to complete the square on y=.5x^2-3x+19/2. i also have to graph this parabola and i dont know how
:
It's easier to complete the square if the coefficient of x^2 is 1
Multiply equation by 2 to get that. I also gets rid of the fraction, you have:
x^2 - 6x + 19 = 0
We want to have the third term value make it a perfect square, so we:
x^2 - 6x + ___ = -19; subtracted 19 from both sides
:
Find the values of the third term, divide the coefficient of x by 2, and square:
6/2 = 3, square 3 and we have 9, we have to add 9 to both sides.
:
x^2 - 6x + 9 = -19 + 9; (x^2-6x+9 is a perfect square)
:
(x - 3)^2 = -10
:
Take the square root of both sides:
x - 3 = +/-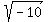
:
We can't have a neg square root, use i, the square root of -1
x - 3 = +/-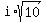
:
x = 3 +/-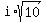 ; add 3 to both sides ; add 3 to both sides
:
The two solutions (this equation does not have any real roots)
x = 3 + 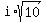 ; ;
and
x = 3 - 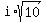 ; ;
:
;
To graph this, assign values to x and find y, a table of values would look like this:
x | Y
-------
-3 | 23
-2 | 17.5
-1 | 13
0 | 9.5
+1 | 7
+2 | 5.5
+3 | 5
+4 | 5.5
+5 | 7
+6 | 9.5
+7 | 13
You should be able to find +8 and +9, as you can see, it is a parabola
Answer by josmiceli(19441)   (Show Source): (Show Source):
|
|
|
| |