|
Question 1208800: Let x and y be nonnegative real numbers. If x^2 + 5y^2 = 30 , then find the maximum value of x + y .
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3828)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 6
Explanation
Let's solve for y in the given equation
x^2 + 5y^2 = 30
5y^2 = 30 - x^2
y^2 = (30 - x^2)/5
y^2 = 6 - 0.2x^2
y = sqrt(6 - 0.2x^2)
Since y is nonnegative, we ignore the negative branch.
The expression
x+y
turns into
x + sqrt(6 - 0.2x^2)
If you were to graph this, and use the calculator's "maximum" feature, then you should find the highest point is located at (5,6).
This shows that the largest value of x+y is 6

Graph of f(x) = x + sqrt(6 - 0.2x^2)
GeoGebra and Desmos are two of many graphing tools to use.
Another way to determine this highest point is to use differential calculus.
Caution: Do not mix up the original y value with the output of the function x + sqrt(6 - 0.2x^2)
-----------------------------------------------------------------------------------------------------
Another approach.
Consider these two sets of numbers
{ a1, a2, a3, ..., an }
{ b1, b2, b3, ..., bn }
Due to the Cauchy-Schwarz Inequality we can state the following

For new students, and perhaps some experienced students as well, this inequality may seem intimidating.
Luckily we only need to worry about sets with 2 items each
{ a1, a2 }
{ b1, b2 }
Allowing us to use an inequality that's far more easier to work with.

Let
 and and 
Square both sides of each equation.
 and and 
The selection of a1 & a2 is to set up x^2+5y^2.
So,


Now we want x+y to show up on the right hand side.
To do this we can say  and and 




 ...... use the fact that x^2+5y^2 = 30 is given to us ...... use the fact that x^2+5y^2 = 30 is given to us




This shows that x+y maxes out at 6
Note that because x,y are nonnegative, we dont need to worry about the plus minus. We focus entirely on the positive square root.
-----------------------------------------------------------------------------------------------------
Yet another approach.
This approach is inspired by tutor ikleyn.
Graph x^2 + 5y^2 = 30 which is an ellipse and graph x+y = c, where c is a parameter.
x+y = c is a family of lines such as x+y=1, x+y=1.5, x+y=1.8, etc.
Here is an interactive Desmos graph where you can move the slider around for c.
https://www.desmos.com/calculator/zyi3ize89w
c = 6 is the largest possible value if we want the blue line to intersect with the red ellipse. The point of tangency is (x,y) = (5,1)
When c > 6, the blue line no longer intersects the ellipse.
Answer by ikleyn(53479)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x and y be nonnegative real numbers. If x^2 + 5y^2 = 30, then find the maximum value of x + y.
~~~~~~~~~~~~~~~~~~
Equation
x^2 + 5y^2 = 30 (1)
represents an ellipse, centered at the origin of the coordinate system.
Equation
x + y = c (2)
represents straight line with the slope -1.
They want you find a point on the ellipse with the maximum value x + y = c.
The value of "c" defines the position of the line in the plane: different values of "c"
produce parallel lines, and changing of the value of "c" moves/translates the lines
vertically up or down, leaving them parallel.
So, they actually want you find the tangent line to the given ellipse with maximum value of "c",
which corresponds to the most high possible position of the tangent line.
Next, since the slope of the line is -1, from geometry intuition, it is clear that
the tangency point on the ellipse lies in the first quadrant.
There is another parallel tangent line, but for this second line the tangency point
is in the third quadrant.
OK. This preface reveals the geometric essence of the problem.
Now I move on to the solution.
All lines x + y = c have the slope -1.
So, we are looking and searching for the points on the ellipse in QI and QIII, where
the tangent line to the ellipse has the slope -1.
For it, I differentiate equation (1)
2x*dx + 10y*dy = 0.
which is the same as
2x*dx = - 10y*dy.
From this equation in differentials, I find the derivative
 = = 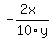 = = 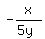 This derivative represents the slope of the tangent line to the ellipse in point (x,y).
I want the slope of the tangent line be -1, the same as for the family of lines (2).
So, I write this equation
This derivative represents the slope of the tangent line to the ellipse in point (x,y).
I want the slope of the tangent line be -1, the same as for the family of lines (2).
So, I write this equation
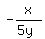 = -1. (3)
Square both sides. You will get = -1. (3)
Square both sides. You will get
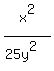 = 1, or x^2 = 25y^2.
I transform the last equation this way, using equation (1)
x^2 = 5*(5y^2) = 5*(30-x^2) = 150 - 5x^2,
x^2 + 5x^2 = 150,
6x^2 = 150,
x^2 = 150/6 = 25,
x = +/- = 1, or x^2 = 25y^2.
I transform the last equation this way, using equation (1)
x^2 = 5*(5y^2) = 5*(30-x^2) = 150 - 5x^2,
x^2 + 5x^2 = 150,
6x^2 = 150,
x^2 = 150/6 = 25,
x = +/-  = +/- 5.
Thus for x= 5, the value of y in the first quadrant is (from equation (1))
5^2 + 5y^2 = 30, ---> 25 + 5y^2 = 30, ---> 5y^2 = 30-25 = 5, y^2 = 5/5 = 1, y = = +/- 5.
Thus for x= 5, the value of y in the first quadrant is (from equation (1))
5^2 + 5y^2 = 30, ---> 25 + 5y^2 = 30, ---> 5y^2 = 30-25 = 5, y^2 = 5/5 = 1, y = 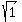 = 1.
For x= -5, the value of y in the third quadrant is (from equation (1))
5^2 + 5y^2 = 30, ---> 25 + 5y^2 = 30, ---> 5y^2 = 30-25 = 5, y^2 = 5/5 = 1, y = - = 1.
For x= -5, the value of y in the third quadrant is (from equation (1))
5^2 + 5y^2 = 30, ---> 25 + 5y^2 = 30, ---> 5y^2 = 30-25 = 5, y^2 = 5/5 = 1, y = -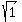 = -1.
Thus, two tangency points are (5,1) in the first quadrant and (-5,-1) in the third quadrant.
For the first point c = x + y = 5 + 1 = 6.
For the second point c = x + y = -5 - 1 = -6.
We want the maximum "c", so we choose the first point with the value of c = 6.
ANSWER. The maximum value of "c" is 6. = -1.
Thus, two tangency points are (5,1) in the first quadrant and (-5,-1) in the third quadrant.
For the first point c = x + y = 5 + 1 = 6.
For the second point c = x + y = -5 - 1 = -6.
We want the maximum "c", so we choose the first point with the value of c = 6.
ANSWER. The maximum value of "c" is 6.
Solved.
|
|
|
| |