Question 1204729: Find the coordinates of the focus and the vertex, the equations of the directrix and the axis of symmetry, and the direction of opening of the parabola.
y^2 - 12x = 0
----------------
This to me looks like a completing the square type problem, but I don't know how to complete a square with only two terms like these.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!


vertex form of your parabola is:
 where ( where ( , ,  ) is vertex and ( ) is vertex and (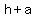 , ,  ) is focus ) is focus
your parabola in vertex form will be:

as you can see,  , ,  , ,  => =>
vertex is at origin ( , , ) )
focus is at ( , ,  )= ( )= (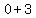 , ,  )=( )=( , , ) )
the axis of symmetry is  => =>
The focus and the directrix lie on either sides of vertex of the parabola and are equidistant from the vertex.
so,  and the equations of the directrix is and the equations of the directrix is

|
|
|