SOLUTION: Write the equation for the ellipse in standard form and general form. foci at (-1,-1) and (9,-1), sum of focal radii 26

From given information about the foci coordinates, you can see that the 
distance between the foci points is 9 - (-1) = 10.


So, the half of this distance is 10/2 = 5 units.


This distance is the eccentricity, which has the standard designation "c".

So, c = 5 units.



Next, since the sum of focal radii is 26, it means that the distance from 
any focus of the ellipse to its any co-vertex is 26/2 = 13.


Thus we have a right angled triangle with one leg of 5 units and the hypotenuse of 13 units.

So, the other leg is 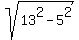  =  =  = 12 units.

Thus we found the minor semiaxis of the ellipse: it is 12 units.

The standard designation for the minor semi-axis of an ellipse is "b".

So, for our ellipse b = 12 units.


Finally, if "a" is the major semi-axis, then we have

     =  - ,

or

     =  - ,

     = 25 + 144 = 169

which implies

    a =  = 13.


Thus the major semi-axis is 13 units long.


Now the standard form of this ellipse equation is

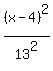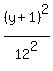     +  = 1.


It is because the center of the ellipse is at the point (4,-1).