|
Question 1191933: Find the equation of the circle tangent to the line 5x + y = 3 at the point (2, -7) and the center is
on the line x - 2y = 19.
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Find the equation of the circle tangent to the line 5x + y = 3 at the point (2, -7) and the center is
on the line x - 2y = 19.
----------------------------------
Step 1, find the slope of the given line.
Step 2, find the equation of the perpendicular bisector of 5x + y = 3 thru the point (2,-7).
Step 3, find the intersection of the given line and the perpendicular bisector.
The intersection is the center of the circle at (h,k).
Step 4, find the distance from the center to the point (2,-7), that's the radius.
===============
 is the circle.
----------------------------
Email via the TY note for help or to check your work.
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website!
A line tangent to a circle is perpendicular to the radius drawn to
the point of tangency. So the radius drawn to the point of tangency
will lie along the line perpendicular to the line 5x + y = 3 that
passes through the point of tangency (2,-7)
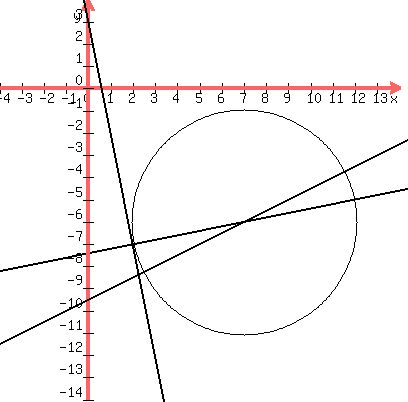We find the equation of the line perpendicular to the line 5x + y = 3 at the
point (2,-7). The line
5x+y=3
y=-5x+3
has slope -5, so a line perpendicular to it has slope which is the negative
reciprocal of -5 which is +1/5. So we find the equation of the line
through (2,-7) with slope 1/5:
  
 
 
 
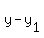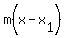
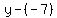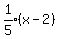
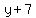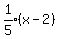
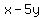
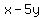We now know that the center lies on the line x - 5y = 37, and we
are given that the center lies on the line x - 2y = 19. So those
lines must intersect at the center of the circle, so we solve them
simultaneously to find their intersection, which is the center of
the circle.
Solve those by substitution or elimination and get x=7, y=-6
So they intersect at (7,-6), the center of the circle.
To find the radius, all we need do is find the distance from the
center (7,-6) to the point of tangency (2,-7). We use the distance
formula:
 
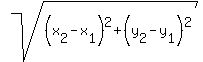
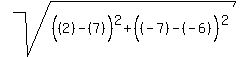
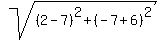
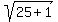
So the radius is and the center is (7,-6).
The equation of the circle is
 
 
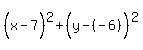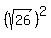
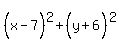Edwin
|
|
|
| |
