|
Question 1183327: A circle is tangent to the line 3x-4y -4 = 0 at the point (-4,-4) and the center is on the line
x+y+7 = 0. Find the equation of the circle
Found 3 solutions by robertb, greenestamps, ikleyn:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  be the equation of the circle. be the equation of the circle.
Note that the point ( , ,  ) is on the line x + y + 7 = 0, hence ) is on the line x + y + 7 = 0, hence  , or , or  . .
Since the point (-4,-4) is on the circle, then the the equation
 is true. This becomes is true. This becomes  after simplifying. after simplifying.
Also,  , or , or  after the fact after the fact  . .
 <==> <==>  . .
Since the point (-4,-4) is on the line 3x - 4y - 4 = 0, and the radial line is perpendicular to this line,
we can find the distance between 3x - 4y - 4 = 0 and the center ( , ,  ). ).
The distance is given by  . .
==> 
==>  , or , or
 , or , or  , or , or  ==> ==>  . .
Then  ==> ==>  . Therefore the center is (-7,0). . Therefore the center is (-7,0).
Also,  . .
Therefore the equation of the circle is  . .
--------------------------------------------------------------------------
This is practically an engineering problem, and some other tutor here might have a much shorter solution.
(Admittedly I'm working from memory on this one.)
From what I remember there is an even shorter formula for a problem like this, but I cannot retrieve that formula.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The circle is tangent to the line 3x-4y-4=0 at the point (-4,-4). The equation of that line in slope-intercept form is y=(3/4)x-1.
To be tangent to y=(3/4)x-1 at (-4,-4), the center of the circle must be on the line perpendicular to y=(3/4)x-1 passing through (-4,-4). A line perpendicular to y=(3/4)x-1 has slope (-4/3). Find the equation of the line with slope -4/3 passing through (-4,-4).




The equation is 
It is given that the center of the circle is also on the line x+y+7=0, or y=-x-7.
We have the equations of two lines, both of which must contain the center of the circle. So find the center of the circle by finding the intersection of those two lines.




The center of the circle is at (-7,0).
The radius of the circle is then the distance from the center (-7,0) to the given point of tangency (-4,-4). A quick sketch, or the distance formula, will show the radius to be 5.
The equation of the circle with center (h,k) and radius r is



ANSWER: The equation of the circle is 
A graph....
red line: 3x-4y-4=0, or y=(3/4)x-1, to which the circle is tangent
green line: (-4/3)x-28/3, perpendicular to the red line passing through (-4,-4)
blue line: x+y+7=0, or y=-x-7, on which the center of the circle must lie
the center of the circle is the intersection of the green and blue lines, (-7,0)

Answer by ikleyn(52792)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Any straight line, perpendicular to the line 3x - 4y - 4 = 0, has an equation
4x + 3y = c,
where c is some constant. The perpendicular line, passing through the point (-4,-4), has the constant "c" equal to
4*(-4) + 3*(-4) = -16 + -12 = -28.
So, the circle center is the intersection of the lines
4x + 3y = -28 (1)
x + y = -7 (2)
It is easy to solve (Elimination or Substitution, on your choice).
The intersection point is y = 0, x = -7.
Thus the center of the circle is the point (x,y) = (-7,0).
The radius of the circle is the distance from its center (-7,0) to the point (-4,-4)
r = 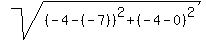 = =  = 5.
Thus the center of the circle is the point (-7,0) and its radius is 5 units.
The standard equation of the circle is = 5.
Thus the center of the circle is the point (-7,0) and its radius is 5 units.
The standard equation of the circle is
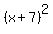 + +  = 25. ANSWER = 25. ANSWER
Solved.
|
|
|
| |