SOLUTION: put the equation 16x^2+y^2+64x-2y+67=0 into conic standard form

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: put the equation 16x^2+y^2+64x-2y+67=0 into conic standard form      Log On


   

Question 1151192: put the equation 16x^2+y^2+64x-2y+67=0 into conic standard form
Found 3 solutions by Edwin McCravy, MathLover1, ikleyn:
Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!
matrix%281%2C3%2C16x%5E2%2By%5E2%2B64x-2y%2B67%2C%22%22=%22%22%2C0%29

Swap the 2nd and 3rd terms on the left to get the terms together
for each letter:

matrix%281%2C3%2C16x%5E2%2B64x%2By%5E2-2y%2B67%2C%22%22=%22%22%2C0%29 

Subtract the constant term from both sides:

matrix%281%2C3%2C16x%5E2%2B64x%2By%5E2-2y%2C%22%22=%22%22%2C-67%29

matrix%281%2C3%2C16x%5E2%2B64x%2By%5E2-2y%2C%22%22=%22%22%2C-67%29

Factor out 16 out of the first two terms, and 1 out of
the last two terms:

matrix%281%2C3%2C16%28x%5E2%2B4x%29%2B1%28y%5E2-2y%29%2C%22%22=%22%22%2C-67%29

We complete the square inside the first parentheses:
1. Multiply the coefficient of x, which is 4, by one-half, getting 2.
2. Square 2, getting 4.
3. Add +4 at the end of the first parentheses.
4. Since the number in front of the parentheses is 16, adding 4 inside
   the parentheses amounts to adding 16∙4 or 64 to the left side, so
   we add 64 to the right side:

matrix%281%2C3%2C16%28x%5E2%2B4x%2B4%29%2B1%28y%5E2-2y%29%2C%22%22=%22%22%2C-67%2B64%29

We complete the square inside the second parentheses:
1. Multiply the coefficient of y, which is -2, by one-half, getting -1.
2. Square -1, getting +1.
3. Add +1 at the end of the first parentheses.
4. Since the number in front of the parentheses is 1, adding 4 inside
   the parentheses amounts to adding 1∙1 or 1 to the left side, so
   we add 1 to the right side:



Next we factor the quadratics in the parentheses:

matrix%281%2C3%2C16%28x%2B2%29%28x%2B2%29%2B1%28y-1%29%28y-1%29%2C%22%22=%22%22%2C-2%29

matrix%281%2C3%2C16%28x%2B2%29%5E2%2B1%28y-1%29%5E2%2C%22%22=%22%22%2C-2%29

This does not represent a conic because the left side is positive
and the right side is negative.  

We get 1 on the right side by dividing each term by -2





We divide top and bottom of the first fraction by 16







If this were a real conic, there would not be a negative number
on the bottom of either term, but only positive numbers.

Did you copy the problem wrong?

Edwin

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

put the equation 16x%5E2%2By%5E2%2B64x-2y%2B67=0+ into conic standard form=> here is an error, to have conic, y%5E2 must be -y%5E2


16x%5E2-y%5E2%2B64x-2y%2B67=0+.......group like terms
%2816x%5E2%2B64x%29-%28y%5E2%2B2y%29%2B67=0+............complete squares
16%28x%5E2%2B4x%2Bb%5E2%29-16b%5E2-%28y%5E2%2B2y%2Bb%5E2%29-b%5E2%2B67=0+
16%28x%5E2%2B4x%2B2%5E2%29-16%2A2%5E2-%28y%5E2%2B2y%2B1%5E2%29-%28-1%29%5E2%2B67=0+
16%28x%2B2%29%5E2-64-%28y%2B1%29%5E2%2B1%2B67=0+
16%28x%2B2%29%5E2-%28y%2B1%29%5E2%2B68-64=0+
16%28x%2B2%29%5E2-%28y%2B1%29%5E2%2B4=0+
16%28x%2B2%29%5E2-%28y%2B1%29%5E2%2B4=0+.... move 16%28x%2B2%29%5E2-%28y%2B1%29%5E2 to the right
4=%28y%2B1%29%5E2+-16%28x%2B2%29%5E2...switch sides
%28y%2B1%29%5E2+-16%28x%2B2%29%5E2=4........both sides divide by 4
%28y%2B1%29%5E2%2F4-4%28x%2B2%29%5E2=1..........write 4 in front of x part as 1%2F%281%2F4%29
%28y%2B1%29%5E2%2F4-%28x%2B2%29%5E2%2F%281%2F4%29=1 => here you have the equation of hyperbola in conic standard form

Answer by ikleyn(52800) About Me  (Show Source):
You can put this solution on YOUR website!
.

Edwin just derived this standard conic equation for you


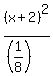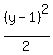    %28x%2B2%29%5E2%2F%28%281%2F8%29%29 + %28y-1%29%5E2%2F2 = -1.


This equation describes the empty set of points.


Indeed, the equation has the left side non-negative (as the sum of two squares), while its right side is the negative number,

so the equation has no real solutions.