|
Question 1150068: A satellite dish is shaped like a paraboloid of revolution. This means that it can be formed by rotating a parabola around its axis of symmetry. The receiver is to be located at the focus. If the dish is 60 feet across at its opening and 5 feet deep at its center, where should the receiver be placed?
How do you find the equation for this parabola?
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
First, we need to derive the equation of the parabola.
Standard form equation of a parabola is y =  .
Since the parabola is 60 feet wide at 5 feet from its vertex, it means that y = 5 at x = 30
5 = .
Since the parabola is 60 feet wide at 5 feet from its vertex, it means that y = 5 at x = 30
5 = 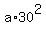 , which implies a = , which implies a =  = = 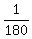 .
Thus the standard equation of the parabola is
y = .
Thus the standard equation of the parabola is
y = 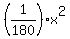 (1)
under given conditions.
Next, it is well known fact that if the parabola has the form y = (1)
under given conditions.
Next, it is well known fact that if the parabola has the form y = 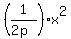 , then the focus of the parabola is at y = , then the focus of the parabola is at y =  (see the lesson Parabola definition, canonical equation, characteristic points and elements at this site).
Comparing it with the equation, we get 2p = 180, i.e. p =
(see the lesson Parabola definition, canonical equation, characteristic points and elements at this site).
Comparing it with the equation, we get 2p = 180, i.e. p =  = 90.
Hence, receiver should be placed on the parabola axis at the distance of = 90.
Hence, receiver should be placed on the parabola axis at the distance of  = = 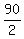 = 45 feet from the vertex. = 45 feet from the vertex.
Solved, explained and completed.
----------------
On parabolas, see the lessons
- Parabola definition, canonical equation, characteristic points and elements
- Parabola focal property
- Tangent lines and normal vectors to a parabola
- Optical property of a parabola
- Practical problems from the archive related to ellipses and parabolas
- OVERVIEW of lessons on parabolas.
in this site.
|
|
|
| |