SOLUTION: I am having trouble with writing an equation of an ellipse, center is at the origin. Focus at (2,0); 7/3 is one-half length of the minor axis.

We plot the center and focus:



So we know that c = 2 since c is the distance 
from the center to the focus.  

We also know that the ellipse is like this 
so its equation is 

We also know that the other focus is 2 units on the 
left of the center, at (-2,0) so we plot that too:



Since we know that 7/3 is one-half length of the minor axis,
that means that that b = 7/3, the semi-minor axis.

So we know that the top point (sometimes called the top covertex)
is (0,7/3), so we plot that too, as well as the other covertex at
(0,-7/3):



The ellipse equation for a,b, and c is , so









That's about 3.073, so we plot the vertices, too,
at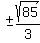 



So the equation 



becomes:





You can simplify it to 



if you like.



Edwin