|
Question 1101661: If the area of the region bounded by the graph of y=x^3, the line x=2 and the x-axis is revolved about the line x=-1 then find the volume of the solid revolution.
Found 2 solutions by Alan3354, greenestamps:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the area of the region bounded by the graph of y=x^3, the line x=2 and the x-axis is revolved about the line x=-1 then find the volume of the solid revolution.
-----------
The limits of x are 0 and 2.
Use shells:
Volume of a shell at x = dx*x^3*2pi*(x+1)
dV = 2pi*(x^4 + x^3)dx
Vol = 2pi*(x^5/5 + x^4/4)
0 --> 0
For x = 2:
Vol = 2pi*(32/5 + 4)
= 104pi/5 cubic units
=~ 65.345 cubic units
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I was hoping another tutor would answer this question, so that I could try to solve it and compare answers. I often have trouble setting up this kind of problem correctly, so I was glad to see another solution.
I did come up with the same answer as the other tutor, but by a different method.
So you can look at the two methods and see if you have a preference for one or the other.
The other tutor used the shell method in his solution. I generally have better luck with the disk method; so that is what I used.
And so that I could visualize the problem better, I found the answer by finding the volume as the volume of a cylinder, minus the volume of the solid of revolution between the curve and the line y=8, instead of finding the volume of the solid of revolution between the curve and the line y=0 (i.e., the x-axis).
So I'm integrating in the y direction from 0 to 8; and my disk has volume 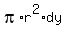 . .
The curve is  ; since I'm integrating in the y direction, I convert this to ; since I'm integrating in the y direction, I convert this to 
Since the rotation is about the line x = -1, the radius r of my disk is 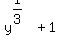
So the volume of my disk is  or or 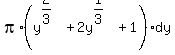 . .
Doing the integration, the volume of my solid of revolution is then pi times 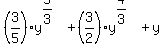 evaluated between 0 and 8. evaluated between 0 and 8.
For y=8: 
and of course 0 for y=0.
The volume of my cylinder is 
So the volume we are looking for in the problem is 
... which is the answer the other tutor got.
|
|
|
| |