|
Question 1082518: An airplane is flying along the hyperbolic
path illustrated in the figure. If an equation of the path
is 2y^2-x^2=8 , determine how close the airplane comes to
a town located at (3,0). (Hint: Let S denote the square of
the distance from a point on the path to(3,0), and
find the minimum value of S.)
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An airplane is flying along the hyperbolic path illustrated in the figure.
If an equation of the path is 2y^2-x^2=8 , determine how close the airplane comes to a town located at (3,0).
(Hint: Let S denote the square of the distance from a point on the path to(3,0), and find the minimum value of S.)
~~~~~~~~~~~~~~~~~~~~~~~
1. Our curve is specific ! If (x,y) is the point on the curve then
2y^2 - x^2 = 8, which implies y^2 = 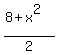 . (1)
2. The distance from ANY point (x,y) on the coordinate plane to the point (3,0) is . (1)
2. The distance from ANY point (x,y) on the coordinate plane to the point (3,0) is
 = = 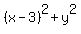 . (2)
Now, if the point lies on the hyperbola, you have (1), and you can substitute this expression for . (2)
Now, if the point lies on the hyperbola, you have (1), and you can substitute this expression for  into the formula (2).
You will get into the formula (2).
You will get
 = =  + + 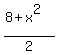 = = 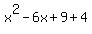 + + 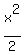 = =  . (3)
So, you need to minimize (3). In other words, you need to find the value of "x" which minimizes this quadratic function.
4. The quadratic function of the general form q(x) = . (3)
So, you need to minimize (3). In other words, you need to find the value of "x" which minimizes this quadratic function.
4. The quadratic function of the general form q(x) =  achieves the maximum at x = achieves the maximum at x =  .
In your case this "x" is x = - .
In your case this "x" is x = - 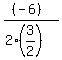 = = 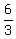 = 2.
So, we found the value of "x". It is x= 2.
Then the corresponding value of "y" on your curve is = 2.
So, we found the value of "x". It is x= 2.
Then the corresponding value of "y" on your curve is
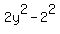 = 8 ----> = 8 ---->  = 8 + 4 = 12 ----> = 8 + 4 = 12 ---->  = =  = 6.
Thus your "closest" point on the curve is (x,y) = ( = 6.
Thus your "closest" point on the curve is (x,y) = ( , , ).
5. Now you can find that minimal distance: ).
5. Now you can find that minimal distance:
 = = 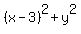 = = 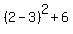 = 1 + 6 = 7.
Hence, the minimal distance itself is = 1 + 6 = 7.
Hence, the minimal distance itself is  = 2.646 (approximately). = 2.646 (approximately).
My congratulations ! The problem is solved.
|
|
|
| |