Question 1079009: Find an equation of an ellipse using the following
center at (2,-2)
vertex at (5,-2)
focus at (3,-2)
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find an equation of an ellipse using the following
center at (2,-2)
vertex at (5,-2)
focus at (3,-2)
~~~~~~~~~~~~~~~~
1. Your prerequisite is the lesson
Ellipse definition, canonical equation, characteristic points and elements
in this site.
2. Notice that the center and the vertices lie in one horizontal line y = -2.
3. The major semi-axis has the length of a = 5-2 = 3.
4. The focal distance is 3-2 = 1.
Hence, 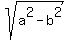 = 1, where b is the minor semi-axis length.
Therefore, = 1, where b is the minor semi-axis length.
Therefore, 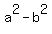 = 1, = 1,  = =  = = 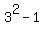 = 8 and b = = 8 and b =  = =  .
4. Finally, the equation of the ellipse is .
4. Finally, the equation of the ellipse is
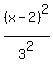 + + 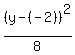 = 1, or = 1, or
 + +  = 1. = 1.
Solved.
|
|
|