Question 1045388: The arch of a bridge is in the shape of a semiellipse, with its major axis at the water level. Suppose the arch is 20 ft. high in the middle, 120 ft. across its major axis. How high above the water level is the arch, at point 20 ft. from the center (horizontally). Round off to 2 decimal places.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! For convenience, I would set my coordinates axes like this:
 . Then the equation of the ellipse is . Then the equation of the ellipse is  for for 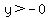 , and we want the value of , and we want the value of  when when  . .
Substituting those values of  into, we get (in both cases) into, we get (in both cases)






There are two solutions, of course,
but we are not interested in  , ,
because that would give you a negative  . .
So,  ---> ---> ---> --->
The approximate value of that number, rounded off the 2 decimal places, is
 . .
so, at point 20 ft. from the center (horizontally) the arch is  above the water. above the water.
|
|
|