Question 1035355: write the equation.
1. hyperbola with foci (0,4) and (0,-4) and asymptotes at y=2x
2. circle passing through the points (12,1) and (2,-3) with center on the line 2x-5y+10=0
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.The major axis is on the line connecting the foci, which is the y-axis.
The center of the hyperbola is halfway between the foci, at (0,0), the origin,
so the minor axis (perpendicular to the y-axis through the center) is the x-axis.
The equation for a parabola centered at the origin, with the y-axis as its major axis is
 with with  and and 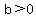 . .
The focal distance,  , is half the distance between the foci. , is half the distance between the foci.
In this case, it is  . .
The semimajor axis,  , is the distance between the center and each vertex. , is the distance between the center and each vertex.
The major axis is the vertical segment connecting vertices (0,-a), (0,a),
which are on the major axis, between the foci, so 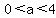 . .
The semi-minor axis is  . .
The asymptotes cross at the center of the hyperbola (in this case (0,0), the origin),
and have equations  and and 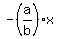 . .
So far, we have

The values  and and  determine a rectangle, determine a rectangle,
passing through the vertices,
with sides measuring  and and 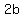 , ,
and diagonals measuring 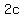 . .
The axes and the asymptotes divide that rectangle into 8 right trianlges with legs  and and  , and hypotenuse , and hypotenuse  , so , so
 . .
Since the asymptotes have equations  and and  , ,
in this case  --> -->  --> -->  , ,
and since  , ,



 . .
So, the equation for the hyperbola in this problem is
 , ,
or  , ,
or  , ,
or  . .
|
|
|