|
This Lesson (Optical property of an ellipse revisited) was created by by ikleyn(52750)   : View Source, ShowAbout ikleyn:
Optical property of an ellipse revisited
This lesson is associated with the lesson Optical property of an ellipse under the current topic in this site. In the referred lesson the proof was presented to the
optical property of an ellipse which was based on the formula for the normal vector to the ellipse and used the scalar products of the focal vectors and the normal vector.
In the current lesson you will find another, more geometric proof based on similarity of triangles. You can read this lesson independently of the lesson
Optical property of an ellipse.
Optical property of an ellipse reads as follows (Figure 1):
If to put the source of light into one of the two ellipse's focus
points and if the internal surface of the ellipse reflects the light
rays as a mirror, then all the light rays emitted by the source
will collect at the second ellipse's focus point.
Figure 1 displays the ellipse with the focus points F1 and F2. A source of light is placed
at the focus point F1. Light rays emitted by the source all arrive to the focus point F2
after reflecting from the ellipse internal surface. You can interchange focuses F1 and F2.
|

Figure 1. Optical property of an ellipse
|
This optical property is equivalent to any of the following geometric facts (Figure 2):
1. For any ellipse's point the angles between the tangent line to the ellipse at this
point and the straight lines drawn from the ellipse foci to the point are congruent.
2. For any ellipse's point the angles between the normal to the ellipse at this point
and the straight lines drawn from the ellipse foci to the point are congruent.
3. For any ellipse's point the normal to the ellipse at this point bisects
the angle between the straight lines drawn from the ellipse foci to the point.
|

Figure 2. To the optical property
of an ellipse ( = = , ,  = = ) )
|
Figure 2 displays the ellipse with the focus points F1=(F,0) and F2=(-F,0), where F is half of the focal distance. The foci are connected with the point M at the ellipse,
which is chosen by an arbitrary way. The tangent line and the normal line at the point M are displayed among with the outward normal shown as the vector n. The optical
property says that
- the angles  and and  between the tangent line and the straight lines drawn from the ellipse foci to the given point are congruent: between the tangent line and the straight lines drawn from the ellipse foci to the given point are congruent:  = = ; ;
- the angles  and and  between the normal line and the straight lines drawn from the ellipse foci to the given point are congruent: between the normal line and the straight lines drawn from the ellipse foci to the given point are congruent:  = = . .
Recall the physical law of reflection: the angle of incidence is equal to the angle of reflection measured from the normal. It is consistent with the geometric optical
properties above.
Let us prove that the angles  and and  are congruent: are congruent:  = = . Consider the right- angled triangles F1EM and F2DM (Figure 3), where F1E and F2D are the . Consider the right- angled triangles F1EM and F2DM (Figure 3), where F1E and F2D are the
perpendiculars drawn from the foci F1 and F2 to the tangent line DE.
The length of the hypotenuse F1M is equal to the length of the focal vector r1 = (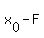 , , ), ),
where ( , , ) are coordinates of the point M at the ellipse. This length was calculated ) are coordinates of the point M at the ellipse. This length was calculated
in the lesson Ellipse focal property in this site. It is equal to |F1M| =  = = 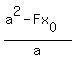 . .
The length of the leg F1E is equal to the distance from the point F1 to the tangent line DE.
The equation of the tangent line to the ellipse at the point M = ( , , ) is ) is
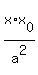 + +  - 1 = 0. (1) - 1 = 0. (1)
|

Figure 3. To the proof of the optical
property of an ellipse  = =
|
in accordance with the lesson Tangent lines and normal vectors to an ellipse in this site. To calculate the distance from the point F1 to the tangent line DE, we need to substitute the coordinates of the point F1 = (F, 0) into the left part of the equation (1) and to divide the result by  = =  (see the lesson The distance from a point to a straight line in a coordinate plane under the topic Introduction to vectors, addition and scaling of the section Algebra-II in this site). By doing this, you will get the expression for the distance (see the lesson The distance from a point to a straight line in a coordinate plane under the topic Introduction to vectors, addition and scaling of the section Algebra-II in this site). By doing this, you will get the expression for the distance
|F1E| =  * *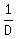 = =  . (2) . (2)
Next, we can make similar calculations for the hypotenuse F2M and the leg F2D.
The length of the hypotenuse F2M is equal to the length of the focal vector r2 = (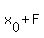 , , ). This length was calculated in the lesson Ellipse focal property: |F2M| = ). This length was calculated in the lesson Ellipse focal property: |F2M| =  = =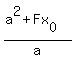 . .
The length of the leg F2D is equal to the distance from the point F2 to the tangent line DE. To calculate this distance, we need to substitute the coordinates of the point F2 = (-F, 0) into the left part of the equation (1). After substitution, you will get the expression for the distance
|F2D| = 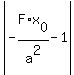 * *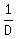 = = 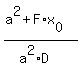 . (3) . (3)
Now, the ratio of the lengths of the leg and the hypotenuse for the triangle F1EM is equal to 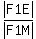 = =  * * = =  . .
The ratio of the lengths of the leg and the hypotenuse for the triangle F2DM is the same:  = =  * * = =  . .
Thus the triangles F1EM and F2DM are similar according to the similarity tests for right-angled triangles (see the lesson Similarity tests for right-angled triangles under the topic Triangles of the section Geometry in this site). Hence, their corresponding angles are congruent:  = = . It is what has to be proved. . It is what has to be proved.
SummaryIn Geometry, the optical property of an ellipse is the set of the following equivalent geometric facts (statements):
1. For any ellipse's point the angles between the tangent line to the ellipse at this
point and the straight lines drawn from the ellipse foci to the point are congruent.
2. For any ellipse's point the angles between the normal to the ellipse at this point
and the focal vectors to the point are congruent.
3. For any ellipse's point the normal to the ellipse at this point bisects the angle
between the focal vectors to the point.
|

Figure 4. The optical property
of an ellipse:  = = , ,  = =
|
The optical property of an ellipse allows another formulation as the bisector property of the tangent line.
4. For any ellipse's point the tangent line to the ellipse at this point bisects the angle
between the focal vector to the point and the continuation of the other focal vector.
The Figure 5 to the right illustrates this property.
The focal radiuses r1 and r2 are continued. The property states that
- the angle  between the tangent line and the continuation of the focal radius r2 is between the tangent line and the continuation of the focal radius r2 is
congruent to the angle  between the focal radius r1 and the tangent line: between the focal radius r1 and the tangent line:  = = ; ;
- the angle 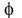 between the tangent line and the continuation of the focal radius r1 is between the tangent line and the continuation of the focal radius r1 is
congruent to the angle  between the focal radius r2 and the tangent line: between the focal radius r2 and the tangent line:  = =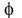 . .
The proof is straightforward. The angles  and and  are congruent as vertical angles. are congruent as vertical angles.
|

Figure 5. The optical property
of an ellipse:  = = , ,  = =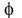
|
From the other side, the angles  and and  are congruent according to the optical property #1 of an ellipse, which is just proved above. are congruent according to the optical property #1 of an ellipse, which is just proved above.
Hence,  = = . Similarly, . Similarly,  = =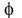 . .
Actually, all four angles are congruent:  = = = = = =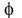 . .
My other lessons on ellipses in this site are
- Ellipse definition, canonical equation, characteristic points and elements
- Ellipse focal property
- Tangent lines and normal vectors to a circle
- Tangent lines and normal vectors to an ellipse
- Optical property of an ellipse
- Standard equation of an ellipse
- Identify elements of an ellipse given by its standard equation
- Find the standard equation of an ellipse given by its elements
- General equation of an ellipse
- Transform a general equation of an ellipse to the standard form by completing the square
- Identify elements of an ellipse given by its general equation
- Standard equation of a circle
- Find the standard equation of a circle
- General equation of a circle
- Transform general equation of a circle to the standard form by completing the squares
- Identify elements of a circle given by its general equation
- OVERVIEW of lessons on ellipses
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.
This lesson has been accessed 4043 times.
|
| |

