Derive an equation and show that the locus of points is a circle
Problem 1
Find the locus of points P(x,y) such that the distance from P to point (3,0) is twice its distance to point (1,0).
Solution
Let (x,y) be the point of this locus.
Then
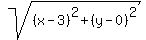 =
= 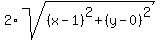 . (1)
The left side is the distance from (x,y) to point (3,0).
The right side is the doubled distance from (x,y) to point (1,0).
Now square both sides of (1). You will get
. (1)
The left side is the distance from (x,y) to point (3,0).
The right side is the doubled distance from (x,y) to point (1,0).
Now square both sides of (1). You will get
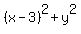 =
= 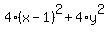 .
Simplify:
.
Simplify:
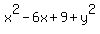 =
= 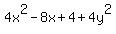 ,
,
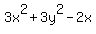 =
=  ,
,
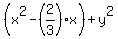 =
=  ,
,
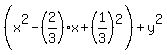 =
= 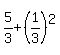 ,
,
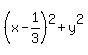 =
=  ,
,
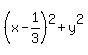 =
= 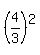 .
It is the standard equation of the circle of the radius
.
It is the standard equation of the circle of the radius  with the center at the point (
with the center at the point ( ,
, ).
Answer. The locus of points under the problem's question is the circle of the radius
).
Answer. The locus of points under the problem's question is the circle of the radius  centered at the point (
centered at the point ( ,
, ).
).
 Circle
Circle 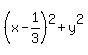 =
= 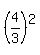
Problem 2
If 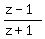 is purely imaginary, then what is the locus of points z ?
is purely imaginary, then what is the locus of points z ?
Solution
The points (1,0) and (-1,0) are selected points in the complex number plane.
For an arbitrary complex number z, the numbers z-1 and z+1 are vectors, connecting z with the points 1 and -1.
The condition that 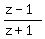 is purely imaginary means that the vectors z-1 and z+1 are perpendicular.
So, the problem asks to find points z in complex plane, such that the "visibilty angle" from z to
these points "1" and "-1" is the right angle.
Or, in other terms, find points z in complex plane, such that the angle between the vectors z-1 and z+1 is the right angle.
Clearly, these points are on the unit circle, and they provide the right angle leaning on the segment [-1,1]
as on the diameter of the unit circle.
Thus the sought locus is the unit circle. The endpoints (-1,0) and (1,0) are not included to the locus.
is purely imaginary means that the vectors z-1 and z+1 are perpendicular.
So, the problem asks to find points z in complex plane, such that the "visibilty angle" from z to
these points "1" and "-1" is the right angle.
Or, in other terms, find points z in complex plane, such that the angle between the vectors z-1 and z+1 is the right angle.
Clearly, these points are on the unit circle, and they provide the right angle leaning on the segment [-1,1]
as on the diameter of the unit circle.
Thus the sought locus is the unit circle. The endpoints (-1,0) and (1,0) are not included to the locus.
Problem 3
If the foci of ellipse 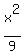 +
+  subtend a right angle at some point P, find the locus of points P.
subtend a right angle at some point P, find the locus of points P.
Solution
The foci of the ellipse 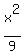 +
+  = 1 are the points (-c,0) and (c,0) on x-axis, where c =
= 1 are the points (-c,0) and (c,0) on x-axis, where c = 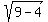 =
=  .
The locus of points P such that the foci subtend the right angle at point P is the circle,
centered at the origin of the coordinate plane and having the radius of
.
The locus of points P such that the foci subtend the right angle at point P is the circle,
centered at the origin of the coordinate plane and having the radius of  ,
EXCLUDING the endpoints of its diameter that lie on x-axis.
,
EXCLUDING the endpoints of its diameter that lie on x-axis.
Problem 4
Find the locus of points representing complex numbers z such that arg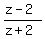 =
=  .
.
Solution
In this problem we have two selected points in the complex plane: A = (-2,0) and B = (2,0).
The complex number z-2 represents a vector connecting point z with the point (2,0).
The complex number z+2 represents a vector connecting point z with the point (-2,0).
Since 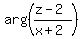 =
=  (given), it means that the angle between the vectors (z-2) and (z+2) is
(given), it means that the angle between the vectors (z-2) and (z+2) is  .
It means that the point z lies on the arc of a circle and the vectors (z-2) and (z+2) form an inscribed angle
of the measure of
.
It means that the point z lies on the arc of a circle and the vectors (z-2) and (z+2) form an inscribed angle
of the measure of  = 60 degrees, which leans on the segment AB as on the chord.
The locus is shown in the Figure below in red line.
The parts of the circles shown in black are not the parts of the locus.
= 60 degrees, which leans on the segment AB as on the chord.
The locus is shown in the Figure below in red line.
The parts of the circles shown in black are not the parts of the locus.

My other lessons in this site on deducing equations for locuses of points are
- Derive an equation and show that the locus of points is a straight line
- Derive an equation and show that the locus of points is an ellipse
- Derive an equation and show that the locus of points is a hyperbola
- Derive an equation and show that the locus of points is a parabola
- OVERWIEW of lessons on deducing equations for locuses of points
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.

