Question 942364: I have a question on the way to find the sides of an isosceles right triangle with a hypotenuse that is radical 72.
I solved the question
"Determine the perimeter of a square with a diagonal of radical 72 centimeters"
To find the perimeter I musty first find the length of the side of the square
Then I set up and equation and turn a segment the square into a triangle using the diagonal as the hypotenuse
I then simplified the equation
I divided by 2
And I found the square roots
I then found the perimeter by multiplying 4 by the value of x
P=26
Instructor comment: When you draw the diagonal through the square, you create a 45-45-90 triangle, where the hypotenuse is radical 72; then you can use those patterns to find the side length of the square to use to find the perimeter.
Please show me the correct way to solve it
Found 3 solutions by josgarithmetic, mananth, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Realize, this triangle is half of a square. The two equal legs and the hypotenuse will fulfill the Pythagorean Theorem relationship equation.
.... you see what to do?
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have a question on the way to find the sides of an isosceles right triangle with a hypotenuse that is radical 72.
I solved the question
"Determine the perimeter of a square with a diagonal of radical 72 centimeters"
To find the perimeter I musty first find the length of the side of the square
Then I set up and equation and turn a segment the square into a triangle using the diagonal as the hypotenuse
I then simplified the equation
I divided by 2
And I found the square roots
I then found the perimeter by multiplying 4 by the value of x
P=26
Instructor comment: When you draw the diagonal through the square, you create a 45-45-90 triangle, where the hypotenuse is radical 72; then you can use those patterns to find the side length of the square to use to find the perimeter.
Please show me the correct way to solve it
You need to find one of the sides of the square before you can determine the perimeter of the square.
Since it’s a square, each side can be named, S
Since  , then we’d have: , then we’d have:  , and you could solve for S. Then you’d be able to find the perimeter. , and you could solve for S. Then you’d be able to find the perimeter.
However, what the professor is saying is that when a 45-45-90 special triangle exists
(and this does occur in a square), and one of the sides is named S, the hypotenuse (the diagonal in this case)
is 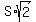 . Now, since it’s given that the diagonal or hypotenuse is . Now, since it’s given that the diagonal or hypotenuse is  , it then follows that: , it then follows that:

 -------- Squaring both sides -------- Squaring both sides




S = 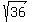 , or 6 , or 6
With S or one side being 6, the perimeter is: 4(6), or  cm cm
|
|
|