Question 738322: Want to make a kite using two rods with fixed length : one of 60cm and one of 40cm.Want to ensure the angle at top corner ( angle ABC ) is a right angle.How far down the rod must you affix the the shorter rod(BE)?
2) What is the smallest available size of material that would be large enough to cut kite shape in 1 whole piece?( Sizes available are squares : 20,40,60,70cm?
3) You want to cut the kite shape out of the square with the top corner(B) aligning with the corner of the square.How far along the side of the square from that corner will you need to cut(to 2 significant figures)?
4)What angle do you need to cut into material?
Please could you help me?
Much Appreciated!!
X
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  AE=EC because the kite is symmetrical. AE=EC because the kite is symmetrical.
1) For angle ABC to measure  , ABE and EBC must measure , ABE and EBC must measure  . .
That means that in the right triangles ABE and EBC, angles EAB and BCE must measure 
In each of those triangles, both acute angles have the same measure, and that means that those triangles are isosceles, with

The shorter rod should be affixed 20cm from the end of the long rod.
2) The surface area of the kite can be calculated as 1200 square centimeters:

A square with 20cm sides is obviously too small.
A square with 40cm sides will have a surface area of
 , which would provide enough material for the kite. , which would provide enough material for the kite.
Can we cut the material in one piece from a 40cm by 40cm square?
Let's see. The 60cm length is hard to accommodate.
The longest straight line segment in a square is the diagonal.
The diagonal splits the square into two isosceles right triangles.
The diagonal is the hypotenuse of those triangles.
In a 40cm by 40cm square, the diagonal's length (in cm) is

That is too short to fit the 60cm length of the kite.
We will need to use the square piece of material measuring
 to a side. to a side.
The diagonal of such a square measures
 , long enough to fit the 60cm length of the kite. , long enough to fit the 60cm length of the kite.
3) If we place B at a corner of the square, sides AB and BC are along the sides of the square. We start cutting along lines AD and CD from points at a distance  from the corner of the square. from the corner of the square.
We can apply the Pythagorean theorem and write
 and since and since  , ,
 --> --> 
That is about  when rounded to 2 significant figures. when rounded to 2 significant figures.
It would be 28.28cm when rounded to 2 decimal places.
4) If we prolong side BC (drawing the side of the square) up to a point P, we can look at the supplementary angles BCD and DCP. Those are the angles made between the edge ot the square of material and the cut to make kite edge CD.
 The measure of angle BCD is the sum of the measures of angles BCE and ECD. We know that angle BCE measures The measure of angle BCD is the sum of the measures of angles BCE and ECD. We know that angle BCE measures 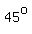 . .
We need to find the measure of angle ECD.
We apply trigonometric ratios to right triangle CDE.

 and we know that and we know that  , so , so
 so ECD measures so ECD measures 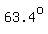 (rounding) (rounding)
and the measure of BCD (rounded) is 
That is the angle of the kite at A an B that we cut from the square of material.
I assume that is the angle meant in the question.
Otherwise, in the material left over we are leaving angle DCP, measuring  . That is the other angle between the cut and the edge of the material. . That is the other angle between the cut and the edge of the material.
|
|
|