Suppose you know one side and two angles, say,
AB = 10, Angle B = 42°, Angle C = 32°
 Draw perpendicular AD from A to BC
Draw perpendicular AD from A to BC

 = sin(42°)
= sin(42°)
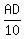 = sin(42°)
AD = 10·sin(42°)
AD = 6.69
= sin(42°)
AD = 10·sin(42°)
AD = 6.69
 = sin(32°)
= sin(32°)
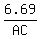 = sin(32°)
AC·sin(32°) = 6.69
AC =
= sin(32°)
AC·sin(32°) = 6.69
AC =  AC = 12.62
Use the Pythagorean theorem to find BD
BD˛ + AD˛ = AB˛
BD˛ = AB˛ - AD˛
BD˛ = 10˛ - 6.69˛
BD˛ = 55.2439
BD = √55.2439
BD = 7.43
Use the Pythagorean theorem to find DC
DC˛ + AD˛ = AC˛
DC˛ = AC˛ - AD˛
DC˛ = (12.62)˛ - (6.69)˛
DC˛ = 114.5083
DC = √114.5083
DC = 10.70
We have side AB = 10, side AC = 12.63, and since we have
BD = 7.43 and DC = 10.70, we have side BC = BD+DC = 7.43+10.70 = 18.13
So we can find the perimeter AB + BC + AC = 10 + 18.13 + 12.62 = 40.75
Edwin
AC = 12.62
Use the Pythagorean theorem to find BD
BD˛ + AD˛ = AB˛
BD˛ = AB˛ - AD˛
BD˛ = 10˛ - 6.69˛
BD˛ = 55.2439
BD = √55.2439
BD = 7.43
Use the Pythagorean theorem to find DC
DC˛ + AD˛ = AC˛
DC˛ = AC˛ - AD˛
DC˛ = (12.62)˛ - (6.69)˛
DC˛ = 114.5083
DC = √114.5083
DC = 10.70
We have side AB = 10, side AC = 12.63, and since we have
BD = 7.43 and DC = 10.70, we have side BC = BD+DC = 7.43+10.70 = 18.13
So we can find the perimeter AB + BC + AC = 10 + 18.13 + 12.62 = 40.75
Edwin