SOLUTION: Starting at the center, designated as C, construct an isosceles right triangle with a congruent leg pointing north from the center, and the other congruent leg pointing east from t

Algebra ->  Pythagorean-theorem -> SOLUTION: Starting at the center, designated as C, construct an isosceles right triangle with a congruent leg pointing north from the center, and the other congruent leg pointing east from t      Log On


   

Question 641702: Starting at the center, designated as C, construct an isosceles right triangle with a congruent leg pointing north from the center, and the other congruent leg pointing east from the top of the first leg. The hypotenuse is at a 45-degree angle pointing northeast from C. Make each congruent leg 2 centimeters in length. Using the hypotenuse of the first triangle as one leg, and another 2-centimeter leg at right angles to it on the outside, construct a second right triangle. Again, the hypotenuse of this new triangle will be a segment coming from C and will point (approximately) east-by-northeast. Repeat, each time using the previous hypotenuse as the longer of the two legs of the new right triangle, and adding a leg of 2 centimeters to the outside end, then forming the new hypotenuse from C. Continue this process until your combined figure has wrapped all the way around the center, so the next triangle you construct overlaps the first one.
Questions
A. What is a common name for this figure?

B. How many triangles were constructed before the algorithm terminated?

C. What is the figure’s total area?
Thank you for any help you can provide!
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
It has four names: Root Spiral, Root Snail, Spiral of Theodorus, and Wheel of Theodorus.



There are 16 triangles poosible before any overlapping occurs.

By using the Pythagorean theorem over and over, the first 
(shortest spoke, the vertical one) has length 2 cm and 
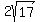the last spoke (longest spoke) has length 2sqrt%2817%29

The sequence of lengths of spokes radiating from center C going
clockwise is:
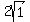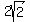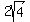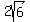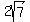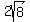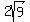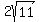2sqrt%281%29cm,2sqrt%282%29cm, 2sqrt%283%29cm, 2sqrt%284%29cm, 2sqrt%285%29cm, 2sqrt%286%29cm, 2sqrt%287%29cm, 2sqrt%288%29cm, 2sqrt%289%29cm, 2sqrt%2810%29cm, 2sqrt%2811%29cm, 2sqrt%2812%29cm, 
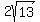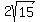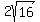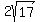2sqrt%2813%29cm, 2sqrt%2814%29cm, 2sqrt%2815%29cm, 2sqrt%2816%29cm,2sqrt%2817%29cm.

[This spiral is usually drawn with the first (vertical spoke being 1 unit
instead of 2 cm. In other words, we could let 1 unit be 2 cm. and then those
spoke lengths would be the square roots of the integers in units, not
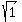centimeters. They would be sqrt%281%29units,sqrt%282%29units, etc., 
sqrt%2817%29units.
I'm sure the reason you were instructed to use 2 cm instead of 1 unit, was 
so that the area would be easier to calculate since there would be no
fractions].

The area of each triangle is found by 1%2F2×(first leg)×(second leg)

The length of the first leg of the 1st triangle is 2
The length of the second leg of the 1st triangle is 2
The area of the 1st triangle is 1%2F2×2×2 = 2 cm²

Area of first triangle = 2cm²

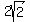The length of the first leg of the 2nd triangle is 2sqrt%282%29
The length of the second leg of the 2nd triangle is 2
The area of the 2nd triangle is 1%2F2×2sqrt%282%29×2 = 2sqrt%282%29 cm²

Area of first two triangles = [2 + 2sqrt%282%29] cm²

The length of the first leg of the 3rd triangle is 2sqrt%283%29
The length of the second leg of the 3rd triangle is 2
The area of the 3rd triangle is 1%2F2×2sqrt%283%29×2 = 2sqrt%283%29 cm²

Area of first three triangles = [2 + 2sqrt%282%29 + 2sqrt%283%29 ] cm²

So you can see that the area of the entire spiral is, after 
factoring out a 2:

A = 

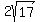[Notice that the last spoke, 2sqrt%2817%29 is not needed since it is
not used to find the area of the 16th triangle]

I get that total area to be 88.9383932 cm². Better check me on that. 

Edwin