SOLUTION: How do I find x and use it to find the unknown sides of a right triangle? Here are the sides: a = x + 2, b = 6x − 1, c = 6x I know I must use the Pythagorean Theorem, I

Algebra ->  Pythagorean-theorem -> SOLUTION: How do I find x and use it to find the unknown sides of a right triangle? Here are the sides: a = x + 2, b = 6x − 1, c = 6x I know I must use the Pythagorean Theorem, I      Log On


   

Question 478385: How do I find x and use it to find the unknown sides of a right triangle? Here are the sides:
a = x + 2, b = 6x − 1, c = 6x
I know I must use the Pythagorean Theorem, I just don't know how to solve this problem.
Found 3 solutions by jorel1380, stanbon, Theo:
Answer by jorel1380(3719) About Me  (Show Source):
You can put this solution on YOUR website!
a = x + 2, b = 6x − 1, c = 6x
(x+2)2+(6x-1)2=(6x)2
x2+4x+4+36x2-12x+1=36x2
x2-8x+5=0
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-8x%2B5+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-8%29%5E2-4%2A1%2A5=44.

Discriminant d=44 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--8%2B-sqrt%28+44+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-8%29%2Bsqrt%28+44+%29%29%2F2%5C1+=+7.3166247903554
x%5B2%5D+=+%28-%28-8%29-sqrt%28+44+%29%29%2F2%5C1+=+0.6833752096446

Quadratic expression 1x%5E2%2B-8x%2B5 can be factored:
1x%5E2%2B-8x%2B5+=+1%28x-7.3166247903554%29%2A%28x-0.6833752096446%29
Again, the answer is: 7.3166247903554, 0.6833752096446. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-8%2Ax%2B5+%29

x=7.3166247903554 or 0.6833752096446
Throwing out the second answer, we get x=7.31662479..

Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
How do I find x and use it to find the unknown sides of a right triangle? Here are the sides:
a = x + 2, b = 6x − 1, c = 6x
I know I must use the Pythagorean Theorem,
----
hypotenuse = 6x
-------
Equation:
(x+2)^2 + (6x-1)^2 = (6x)^2
------
x^2+4x+4 + 36x^2-12x+1 = 36x^2
-----
x^2-8x+5 = 0
---
x = [8 +- sqrt(64 - 4*5)]/2
---
x = [8 +- sqrt(44)]/2
---
x = [4 +- 2sqrt(11)]
Positive solution:
x = 4 + 2sqrt(11)
----
6x = 24+12sqrt(11)
6x-1 = 23+12sqrt(11)
x+2 = 6 + 2sqrt(11)
=========================
cheers,
Stan H.

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
the pythagorean formula is:
hypotenuse squared = first leg squared plus second leg squared.
the hypotenuse is the side opposite the 90 degree angle.
each leg is opposite one of the other angles of the triangle.
since it's a right triangle, those other 2 angles will be acute (less than 90 degrees) and their sum will be equal to 90 degrees (sum of the angles of a triangle is 180 degrees).
looks like your triangle has been labeled ABC and it looks like angle C is the right angle (90 degree angle) because side c, which is opposite angle C, is the largest side.
a is one of the legs
b is the other of the legs
c is the hypotenuse.
the pythagorean formula becomes:
c^2 = a^2 + b^2
since a = x+2 and b = 6x-1 and c = 6x, then this formula becomes:
(6x)^2 = (x+2)^2 + (6x-1)^2
this becomes:
36x^2 = x^2 + 4x + 4 + 36x^2 - 12x + 1
combine like terms to get:
36x^2 = 37x^2 - 8x + 5
subtract 36x^2 from both sides of this equation to get:
0 = x^2 - 8x + 5
this is the same as:
x^2 - 8x + 5 = 0
the standard form of a quadratic equation is ax^2 + bx + c = 0
this equation is in the standard form which means that:
a = 1
b = -8
c = 5
use the quadratic formula to solve for the roots of this equation.
the quadratic formula is:
x = 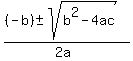%28%28-b%29%2B-sqrt%28b%5E2-4ac%29%29%2F%282a%29
plugging the values for a and b and c in this equation gets:
x = 7.31662479
or:
x = .68337521
since we know the value of x, we can now find the sides of this right triangle.
using x = 7.1662479, we get:
a = x + 2 = 9.31662479
b = 6x - 1 = 42.89974874
c = 6x = 43.89974874
using x = .68337521, we get:
a = x + 2 = 2.68337521
b = 6x - 1 = 3.100251258
c = 6x = 4.100251258
if these numbers are good, then a^2 + b^2 = c^2 should hold true.
plugging those numbers into the equation proves that the equation is true for both values of x, confirming that these values of x are good.
The sides of the triangle can be either the first set given for when x = 7.16, or the second set given for when x = .68.
the actual numbers, without rounding, have been used in all calculations.
the angles of your right triangle can be found using the law of sines.
that law states that:
a/sin(A) = b/sin(B) = c/sin(C)
we know that C is equal to 90 degrees which means that the sine of C is equal to 1.
to solve for angle B, we would use this ratio as follows:
b/sin(B) = c/sin(C) which becomes:
42.89974874/sin(B) = 43.89974874/1
cross multiply to get:
43.89974874*sin(B) = 42.89974874
divide both sides of this equation by 43.89974874 to get:
sin(B) = 42.89974874/43.89974874 = .977220826
this makes angle B equal to 77.7472243
this makes angle A equal to 90 - 77.7472243 = 12.2527757
if we used the second set of values for a, b, and c, then we would get the following for angle A and angle B.
using:
b = 6x - 1 = 3.100251258
and:
c = 6x = 4.100251258
we get:
3.100251258/sin(B) = 4.100251258/1
multiply both sides of this equation by sin(B) and divide both sides of this equation by 4.100251258 to get:
sin(B) = 3.100251258/4.100251258 which gets:
sin(B) = .756112507
this makes angle B equal to 49.12267335 degrees.
this makes angle A equal to 90 - 49.12267335 = 40.87732665 degrees.
the picture below shows you what both of your triangles would look like.
$$$$$