Question 246443: THE HYPOTENUSE OF A RIGHT TRIANGLE IS 1 INCH LONGER THAN ONE LEG AND 8 INCHES LONGER THAN THE OTHER. FIND THE LENGTH OF EACH SIDE OF THE TRIANGLE.
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! right triangle
c^2=a^2+b^2
where c is the hypotenuse and a and b are the legs.
c=a+1
solve for a
a=c-1
c=b+8
solve for b
b=c-8
substitute
c^2=(c-1)^2+(c-8)^2
(c-1)^2=c^2-2c+1
(c-8)^2=c^2-16+64
c^2=2c^2-18c+65
subtract c^2
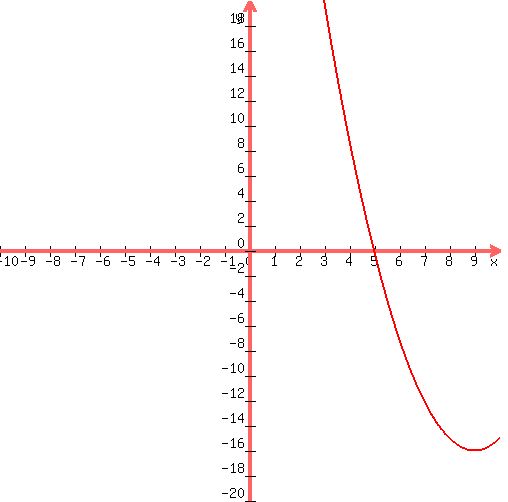
c^2-18c+65=0
13 and 5
13,12, 5
5,4,-3
but -3 can't be a side of a triangle
so we have 13, 12, and 5
13 is hypotenuse
12 and 5 are the legs
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=64 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 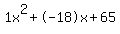 can be factored: can be factored:

Again, the answer is: 13, 5.
Here's your graph:
 |
|
|
|