Question 174426: c=x+8
b=x
a=x+7
find x
i tried everything i could..i cudnt find any solutions and it drove me crazy...help would be soo appreciated.
Found 4 solutions by josmiceli, stanbon, Electrified_Levi, Edwin McCravy:
Answer by josmiceli(19441)   (Show Source):
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! c=x+8
b=x
a=x+7
find x
------------
x = c-8
x = a-7
=========
c-8 = a-7
c = a + 1
--------------
Solutions: All ordered pairs (a,c) where c=a+1
Therefore : x = c-8 = (a+1)-8 = a-7
-------------
Final solution: x = a-7
and b = a-7 since x = b.
=============================
Cheers,
Stan H.
Answer by Electrified_Levi(103) (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
If this is a Pythagorean Theorem, this is how you would find "x"
.
c=x+8
.
b=x
.
a=x+7
.
find x
.
Pythagorean Theorem is 
.
Now replace the letters "a", "b", and "c" with what they equal in "x" terms
.
Replace "a" with (x+7)
.
Replace "b" with (x)
.
Replace "c" with (x+8)
.
=  , now you would just solve for "x"
.
=  , you would now use the FOIL meathod to multiply
.
=  =  =  = 
.
 =  =  , Now we will combine like terms
.
=  , we will now move everything on the right side to the left side
.
=  =  , now we have a quadratic equation
.
We will solve using the quadratic equation
.
Quadratic equation = 
.
Quadratic equations are in the form 
.
,
.
In our equation
.
a = 1
.
b = (-2)
.
c = (-15)
.
Now replace these letters with the numbers in the quadratic equation
.
=  =  =  =  = 
.
 =  = 
.
 =  = 
.
You can check by replacing these numbers into the original quadratic equation
.
(5), =  =  =  (True)
.
(-3), =  =  = ( True )
.
We could have used factoring to solve, but this only works sometimes
.
.
We could have listed all of the factors of (-15), the two factors would have to equal (-2)
.
We would start like this
.
( x )( x )
.
(1, -15) ( added = (-14))
.
( 5, -3) ( added = 2 )
.
( ,  ) ( added = (-2))
.
The factors would then be
.
( x + 3 )( x - 5) = 0
.
You would then set each factor equal to "0"
.
 =  =  = 
.
 =  =  = 
.
These are our two answers/solutions
.
You can check even further if we replaced "x" in our very original equation
.
(5), =  =  =  =  (True)
.
(-3),  =  =
 =  ( True )
.
Don't be fooled with your two answers, since this is a triangle, your answer cannot be negative ( you cannot have negative sides ), so (-3) is not an answer
.
The only answer that works is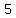 
.
.
Hope I helped, Levi
Answer by Edwin McCravy(20055)  (Show Source):
You can put this solution on YOUR website! c=x+8
b=x
a=x+7
find x
i tried everything i could..i cudnt find any solutions and it drove me crazy...help would be soo appreciated.
There are infinitely many solutions.
1. Pick any number you want for x to be.
2. Add 8 to what you picked for x and you have c.
3. b is that same number you picked for x.
4. Add 7 to what you picked for x and you have a.
Suppose you pick x=4.
Then add 8 and you have c=12
Then b is the same as x, so b=4
Then add 7 to the 4 you picked for x and so a=11.
So a=11, b=4, c=12, x=4
Lets check by substituting in
c=x+8
b=x
a=x+7
12=4+8 that checks
4=4 that checks
11=4+7 that checks
------
Suppose you pick x=100.
Then add 8 and you have c=108
Then b is the same as x, so b=100
Then add 7 to the 100 you picked for x and so a=107.
So a=107, b=100, c=108, x=100
Lets check by substituting in
c=x+8
b=x
a=x+7
108=100+8 that checks
100=100 that checks
107=100+7 that checks
-------
Suppose you pick x=-7.3689
Then add 8 and you have c=.6311
Then b is the same as x, so b=-7.3689
Then add 7 to the -7.3689 you picked for x and so a=-.3689
So a=-.3689, b=-7.3689, c=.6311, x=-7.3689
Lets check by substituting in
c=x+8
b=x
a=x+7
.6311=-7.3689+8 that checks
-7.3689=-7.3689 that checks
-.3689=-7.3689+7 that checks
There are infinitely many solution sets for a,b,c,x.
There's not just one.
Edwin
|
|
|
