Question 145431: The sum of the lengths of the diagonals of a rhombus of side 61 cm is 142 cm. What is (a) the difference in the lengths of the diagonals, (b) the area of the rhombus?
i can't get the solution out of it as i think i do not have enough informantion so i do not know how to solve it.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! The sum of the lengths of the diagonals of a rhombus of side 61 cm is 142 cm. What is (a) the difference in the lengths of the diagonals, (b) the area of the rhombus?
i can't get the solution out of it as i think i do not have enough informantion so i do not know how to solve it.
Yes, there's enough information. First we draw a rhombus with 61cm sides:

Now draw in the longer diagonal and label its length x cm.

Now take away the bottom half of the rhombus,
and you have an isosceles triangle. Label the
angle  : :

We use the law of cosines:


That's one equation we will use.
Now let's go back to the original rhombus.

Since two angles of a parallelogram
which are next to each other are
supplementary, we label the angle
 ° °
Now we draw the other diagonal and label its length y cm:

Take away the right half and we have
another isosceles triangle.

We use the law of cosines again:


Now we use the fact that 

or

Take that equation with the other one:


Now we add equals to equals. Adding
the left sides gives  and and
adding the right sides, the cosine terms
cancel out. So we have:

Now we are told that the sum of the diagonals
is 142 cm., so we have the equation

So we have this system of equations:


Can you solve that by solving the second for
one of the letters and substituting into the
first equation? If not post again asking
how.
Solution to that system of equations:  , , 
Those are the lengths of the diagonals.
The difference is just  . .
Now since the diagonals of a rhombus are
perpendicular bisectors of each other, the
shorter diagonal, which is 22 cm is bisected
by the long diagonal, and so each half is
11 cm.

To find the area, take away the bottom half, and
we have this triangle to find the area of:

The base of that triangle is 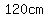 , and its , and its
height is 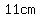

So we double that to find the total area of the rhombus.
Answer = 
Edwin
|
|
|