SOLUTION: Please help me with this one. The lengths of the diagnols of a rhombus are inthe ratio 2:1. If the perimeter of the rhombus is 20, find the sum of the lengths of the diagnols.

Discussion





The diagonals of a rhombus are perpendicular bisectors, so half of one diagonal

half of the other diagonal, and one of the sides of the rhombus form a right

triangle with the rhombus side being the hypotenuse.





Since we know the perimeter and we know that all four sides of the rhombus are

equal, we can calculate the length of the triangle hypotenuse by dividing the

rhombus perimeter by 4.





Since the diagonals mutually bisect each other and the length of the diagonals

are in the ratio 2:1, the measures of the half-diagonals that form the legs of

the triangle must also be in the ratio 2:1.





From here, we can apply the Pythagorean theorem to determine the lengths of the

half-diagonals.







Solution





If we let x be a representation of the measure of the short leg of the triangle

then the measure of the long leg must be represented by 2x.





The perimeter is given as 20, so the length of one side of the rhombus is:







Using Pythagoras,



















So the measure of the short leg of the triangle is  and the 

measure of the short diagonal is 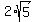.  The measure of the long

leg of the triangle is twice the short leg, or 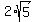 so the measure

of the long diagonal is .



 is then the sum of the lengths of the diagonals.