SOLUTION: In ∆ACS, AC = 12, SA = 8 and SC = 16. Determine the measures of all the interior angles of the triangle.

Use the cosine law

    c^2 = a^2 + b^2 - 2bccos(C),

where "a", "b", "c" are the lengths of the three sides of a triangle, and C is the angle opposite to the side "c".


It gives

    cos(C) = .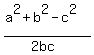


Apply this formula to each angle of the triangle


    angle A, a= 12, b= 8, c= 16;  cos(A) = 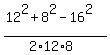 = -0.25;

                                  A = arccos(0.25) = 1.823 radians = 104.48 degrees.


    angle C, a= 12, b= 16, c= 8;  cos(A) = 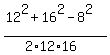 = 0.875;

                                  C = arccos(0.875) = 0.505 radians = 28.96 degrees.


    angle S, a= 8, b= 16, c= 12;  cos(S) = 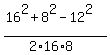 = 0.6875;

                                  C = arccos(68.75) = 0.813 radians = 46.57 degrees.


The problem is just solved: all the angles are found.


As a conclusion, I will check the sum of angles  104.48 + 28.96 + 46.57 = 180 degrees,   ! correct !