SOLUTION: ABCD is a square with diagonal AC 8 units long. How many square units are there in the area of the square?

If "a" is the side length of a square, then the square of its diagonal is


   a^2 + a^2 = 2a^2,  according to Pythagoras.


From the other side, the area of such a square is a^2.


So, to calculate the area in your case, you need to square the diagonal and then divide it by 2:


    Area =  =  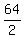= 32 square units.


Answer.  The area of the given square is 32 square inches.

The diagonals divide the square in 4 congruent right angled triangles with the legs of the length 4 unit each.


So the area of each such triangle is   = 8 square units.


Then the area of the entire square is 4 times it, i.e. 4*8 = 32 square units - the same answer.