Question 1106199: How far up a wall will a 25 foot long ladder reach if the bottom must be at least 6 feet from the bottom of the wall? What will be the slope of the ladder if the bottom is 6 feet from the wall? What angle will the ladder make with the ground?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Assuming the ground is horizontal, and the wall surface is vertical,
you have a right triangle with the ladder as its hypotenuse.
According to the Pythagorean theorem,
if the ladder is exactly 6 ft from the bottom of the wall,
the top of the ladder will be  feet above the ground, with feet above the ground, with





So the ladder could reach about 24 ft 3 inches.
For practical purposes, I would say 24 feet.
If the ladder top touches the wall  feet above the ground, feet above the ground,
with the bottom of the ladder 6 ft from the wall,
the slope of the ladder is
  . .
That slope is the tangent (opposite side divided by adjacent side)
of the angle will the ladder makes with the ground.
So, the calculator will tell you that an acute angle with a tangent of 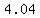 measures about measures about
 . .
All of the answers are numbers that cannot be expressed as exact decimals,
so approximate answers is all you can get.
Those are good enough for real life,
and hopefully accepted by any teacher.
|
|
|