SOLUTION: start with an equilateral triangle ABC of a side of 2 units and construct three outward-pointing squares ABPQ, BCTU, CARS and the three sides AB, BC and CA. what is the area of the

Algebra ->  Pythagorean-theorem -> SOLUTION: start with an equilateral triangle ABC of a side of 2 units and construct three outward-pointing squares ABPQ, BCTU, CARS and the three sides AB, BC and CA. what is the area of the      Log On


   

Question 1066618: start with an equilateral triangle ABC of a side of 2 units and construct three outward-pointing squares ABPQ, BCTU, CARS and the three sides AB, BC and CA. what is the area of the hexagon PQRSTU?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The hexagon is made up of
1 central equilateral triangle of side length 2,
3 squares of side length 2, and
3 isosceles triangles sharing sides of length 2 with the squares.
The surface area of each square is 2%5E2=4 .
The surface area of any triangle ABC can be calculated as
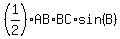%281%2F2%29%2AAB%2ABC%2Asin%28B%29 .
For the central, equilateral triangle ABC,
all sides have equal length, and all angles have the same measure:
AB=BC=AC=2 and A=B=C=60%5Eo .,
so .
The angle between the squares measures
120%5Eo=360%5Eo-%2890%5Eo%2B60%5Eo%2B90%5Eo%29 ,
because it completes 360%5Eo when added to
the right angles of two squares,
plus a 60%5Eo angle of the central equilateral triangle.
So each of the three outside isosceles triangles have
two sides of length 2 flanking an angle measuring 120%5Eo ,
so the area of each of those 3 isosceles triangles is
.
Since the area of the hexagon is the sum of the areas of
3 squares, each with area%28square%29=4 ,
and 4 triangles, each with area%28triangle%29=sqrt%283%29 ,
area%28hexagon%29=3%2A4%2B4%2Asqrt%283%29=highlight%2812%2B4sqrt%283%29%29 .