SOLUTION: A diagonal of a rhombus, of which the sides are 52cm, is 48cm. What is the length of the other diagonal? (In 1 decimal place) Thx.

Algebra ->  Pythagorean-theorem -> SOLUTION: A diagonal of a rhombus, of which the sides are 52cm, is 48cm. What is the length of the other diagonal? (In 1 decimal place) Thx.      Log On


   

Question 1040565: A diagonal of a rhombus, of which the sides are 52cm, is 48cm. What is the length of the other diagonal? (In 1 decimal place)
Thx.
Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.
A diagonal of a rhombus, of which the sides are 52cm, is 48cm. What is the length of the other diagonal?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Solution 1 

Diagonals of a rhombus divide it in four congruent right-angled triangles.
By considering one such a triangle, we know its hypotenuse (52 cm) and one of two legs (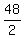48%2F2 = 24 cm). 
Then we can find the other leg as sqrt%2852%5E2+-+24%5E2%29 = sqrt%282128%29 = 46.13 cm (approximately)
So, 46.13 cm is half of the unknown diagonal and 92.26 cm is the entire diagonal length.

Answer.  The length of the other diagonal is about 92.26 cm.

Solution 2 

If "a" is the length of the rhombus side and "c" and "d" are the lengths of its diagonals, then

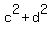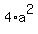c%5E2+%2B+d%5E2 = 4%2Aa%5E2.

See the lesson The length of diagonals of a rhombus in this site.

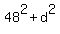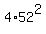Hence, 48%5E2+%2B+d%5E2 = 4%2A52%5E2, where d is the length of the other diagonal.

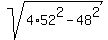Then d = sqrt%284%2A52%5E2-48%5E2%29 = 92.26 cm (approximately).

We have the same answer as in the Solution 1.