SOLUTION: The right triangle has a square attached to its hypotenuse.What is the perimeter of the triangle?Give your answer to the nearest tenth of a centimetre. square = 914 cm2 traiang

Hello,

the hypotenuse of your triangle is .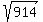

It is not integer (whole) number, it is not rational, it is irrational.

Now, draw the circle on this hypotenuse as on the diameter ( taking the radius of the circle equal to half of  ).

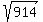Any triangle inscribed to this circle and leaning on this diameter is a right-angled triangle.

So, any of these triangles satisfy the condition you submitted. But these triangles have different perimeters.

So, your problem has no unique solution.
In opposite, it has infinitely many solutions.

Is it what you want?

I think it is not what you want.

I think that your condition (your claim) is incorrect, is wrong.

Now, it is not my duty to explain you why your claim is wrong.
It is your responsibility to provide the correct condition.
Think when (and before) you submit your claims.