Questions on Logic: Proofs answered by real tutors!

Tutors Answer Your Questions about Proofs (FREE)

Question 1079556: Can you help me with this assignment in analytic geometry:

The segment joining (2,-4) and (9,3) is divided into two segments, one of which is � as long as the other. Find the point of division.
I need a complete solution. Can you graph it. Thank you!
Click here to see answer by Edwin McCravy(20054)

Question 1079557: Can you help me with this assignment in analytic geometry:

Show that each of the points are the vertices of a rectangle
L ( -4,3); M (0,-2); N(5,2); O (1,7)
I need a complete solution. Can you graph it. Thank you!
Click here to see answer by Boreal(15235)

Question 1079739: If the slope of the line determined by the points (x,5) and (2,8) is -3, find x?
Click here to see answer by josmiceli(19441)

Question 1079736: Can you help me with this assignment in analytic geometry:
The distance between points (2,0) and (, 3) is square root of 34, find x
I need a complete solution. Can you graph it. Thank you!
Click here to see answer by josgarithmetic(39616)

Question 1079740: Graph the linear equation x-2y-4=0
Click here to see answer by josgarithmetic(39616)

Question 1079738: The y intercept of the equation of a line is 5x+2y-1=0
Click here to see answer by josgarithmetic(39616)

Question 1080118: How to prove is divisible by 2 using mathematical induction given it's true for all natural numbers (n)?
Click here to see answer by Edwin McCravy(20054)

Question 1080223: I need help with this mathematical induction to show that the given statement is true for all natural numbers,
3 + 5 + 7 +...+ (2n+1) = n(n+2)
So far I have the following:
Prove Basis n=1
n(n+2)
= 1(1+2)
= 3
Therefore the statement is true for n=1.
When n=k assume
3 + 5 + 7 +...+ (2n+1) = n(n+2)
replace n with k
3 + 5 + 7 +...+ (2k+1) = k(k+2)
Then n = k+1 must be proven, meaning replace k terms with (k+1)
---------------------------------------------------------------------------------
This is where I get lost, I don't know where/how I should replace with (k+1) despite how simple it sounds
I get
3 + 5 + 7 +...+ (2(k+1)+1) = (k+1)((k+1)+2)
But some sites show a funky set up where the right/first part of the equation gets another (k+1) replacement but don't explain how. I'm sure the left hand side (k+1)((k+1)+2) is correct. I know that after that step you must replace the 3 + 5 + 7 ... etc. but I can't get that far since I'm stuck on the (k+1) replacement! Any help/advice is appreciated and I don't need it solved just some guidance! Thank you!
Click here to see answer by jim_thompson5910(35256)

Question 1080517: Using mathematical induction, show its true for all natural #'s n
+ =
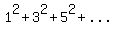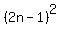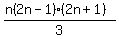
So far I got
Proof n=1
=
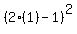1 = 3/3
1 = 1
so its true for n=1
next assume n = k, so
+ =
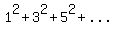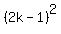then we must prove n = k+1
+ + =
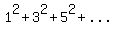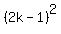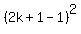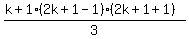
we do some replacing with our n = k

+ =
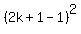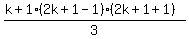
we have our left hand side that we must match to our right hand side, but this is where my math get's messy when I go to simplify,
+ =
+ =
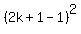now I'm left with a +4k^2 and I'm unsure what method to use here, or maybe I did the first steps wrong? If I factor the k(2k-1)(2k+1) I get a 4k^3-k and I thought maybe multiply by (3/3) to get everything as denominator of 3, but it doesn't really help me understand what I should do next for certain. Any help would be greatly appreciated
Click here to see answer by ikleyn(52775)

Question 1083301: The sum of two numbers is 93. The larger number is 3 more than 5 times the smaller number. Find the numbers.

Click here to see answer by josgarithmetic(39616)

Question 1083625: P ∙ (Q ⊃ R) ; (P ∙ Q) ⊃ (P ∙ R)
are logically equivalent to each other, or whether they are contradictory to each other by making a truth table for them. If they are neither of those, determine whether they are consistent with each other, or whether they are inconsistent with each other
Click here to see answer by jim_thompson5910(35256)

Question 1086495: p->negation q , q disjunction r , negation s , negation r is a valid inference

Click here to see answer by Edwin McCravy(20054)

Question 1087176: I AM STUCK NOW.
12. (A → B) & (A → C) ├ A→ (B & C)
1) (A → B) & (A → C) A
2) A PA
3) (A → B) 1 & O
4) (A → C) 1 & O

Click here to see answer by jim_thompson5910(35256)

Question 1087187: P v Q, P → (T → S), P → T, S ↔ Q ├ S
1. P v Q A
2. P → (T → S) A
3. P → T A
4. S ↔ Q A
5. P 1 v O
6. Q 1 v O
7. S →Q 4 ↔ O
8. S 7, 6 → O
Do I have all of the steps completed?

Click here to see answer by jim_thompson5910(35256)

Question 1087594: Kv~M, (K>~Z)>(~M>K), (Kv~M)>(K>~Z) / ~ZvK
Click here to see answer by Edwin McCravy(20054)

Question 1088290: If 7x-5y=20and12x+5y=75 xy=?

Click here to see answer by Fombitz(32388)

Question 1088315: 1. ~Fv~G
2. ~F ⊃ Z
3.~G ⊃ ~R
4. (Zv~R) ⊃ (U ⊃ P)
5. ~P. /~U
Click here to see answer by jim_thompson5910(35256)

Question 1088314: Create a proof for the following argument
1. M ⊃ H
2.(K ∨ F) ⊃ M
3.K /H
Click here to see answer by Edwin McCravy(20054)

Question 1089635: ~M, (~M � ~N) → (Q → P), P → R, ~N, therefore, Q → R
Click here to see answer by math_helper(2461)

Question 1089639: ~(Z v Y) → ~W, ~U → ~(Z v Y), (~U → ~W) → (T → S), S → (R v P), [T → (RvP)] → [(~R v K) � ~K], therefore, ~K
Click here to see answer by math_helper(2461)

Question 1089734: Help! I need this badly. Use rules of inference and replacement. Thaaaanks!
P > A
X > B
/(P v X) > (A v B)
Click here to see answer by math_helper(2461)

Question 1090173: How do I solve ~Q → (L → F), Q → ~A, F → B, L, therefore, ~A v B with either reductio ad absurdum or conditional proof?
Click here to see answer by jim_thompson5910(35256)

Question 1090484: Need help solving this proof:
1. ~O � K
2. ~O >(~R v A)
3. (~R > ~W) � (A > G)
4. (~W > O) � (G > Z)
/ Z

Thanks!!
Click here to see answer by jim_thompson5910(35256)

Question 1090491: Stuck on this problem:
1. ~A > (M > A)
2. (Z > M) � (X = R)
3. ~A
/ ~Z v I

Click here to see answer by jim_thompson5910(35256)

Question 1090580: What is the smallest integer u, for which 5u > 625?
Click here to see answer by Edwin McCravy(20054)

Question 1090514: Help!
1. ~M�(Z > R)
2. (~M v G) > ~ U
3. (~M v ~X) > ~B
4. (~B � ~U ) > (E > M)
/ ~E
Click here to see answer by Edwin McCravy(20054)

Question 1090652: Proof:
1. ~O > ~ O
2. X > (X > O)
/~X
Click here to see answer by jim_thompson5910(35256)

Question 1090916: Proof for:
1. U v (~U > ~B)
2. ~B > (R > U)
3. ~U
/ ~R
Click here to see answer by Edwin McCravy(20054)

Question 1091271: I need some help with this question. I am confused as to how to write this out, please show me how you get to each step.
Regular Proof:
1.(D*E)v(~D*~E)
2.(H*J)>~(D=E)
3.~~HvJ / J=~H
Thanks!
Click here to see answer by jim_thompson5910(35256)

Question 1092345: Induction
1^3+3^3+5^3+...+(2n-1)^3 = 2n^4-n^2
Click here to see answer by ikleyn(52775)

Question 1092548: Show
Click here to see answer by Alan3354(69443)

Question 1096901: Hello, I am stuck on these two logic proofs and would love some guidance.

Click here to see answer by richwmiller(17219)

Question 1097430: What are the proofs for the following 5
Click here to see answer by richwmiller(17219)

Question 1097983: 1. (E ⊃ A) � (F ⊃ A)
2. E ∨ G
3. F ∨ ∼G / A

Click here to see answer by Edwin McCravy(20054)

Question 1098441: If a number is divisible by 8, then it is also divisible by 16. Is this true or false? Please explain.
Click here to see answer by richwmiller(17219)

Question 1099349: Please help!
A ⊃ B
A ⊃ (B ⊃ C)
B ⊃ (C ⊃ D)
∴ A ⊃ D

Click here to see answer by Edwin McCravy(20054)

Question 1099348: Please help me with this proof! thank you in advance.
A -> (C \/ B)
~(D \/ C)
~(E \/ B)
∴ ~A

Click here to see answer by Edwin McCravy(20054)

Question 1100027: How I determine the validity of the argument using the truth table.
If you invest in business, then you get profit.
You didn't invest in business.
Therefore, you didn't get profit.

Click here to see answer by richwmiller(17219)

Question 1101171: Construct proofs to show that the following arguments are valid.
1.(AvG)>K
2.K>(B>F)
3.A.B ... (Conclusion is triple dot) F
So far I've got
4. (AvG)>(B>F) 1,2 Hypothetical syllogism
5. B 3, Simplification
6. A 3, Simplification
I have to prove how F is the conclusion.
Click here to see answer by Edwin McCravy(20054)

Question 1101165: Classify the following statement, using any technique you can: ~A ∨ (B ⊃ A)

Consistent

Contingent statement

Tautology

Self-contradiction
Click here to see answer by Edwin McCravy(20054)

Question 1101290: Today I asked my Professor in my Logic class if I could do this.
1. ~P
2. ~(PvQ)>~R
3. ~Q ...(conclusion) ~R
4. ~Pv~Q 1,Add
5. ~R 2,1 MP
He flipped out and asked how in the world did I got this because ~Pv~Q is not the same as ~(PvQ). He very rudely told me I should know this by now. Which I obviously don't and was curious why those are not equivalent and if they ever would be equivalent. Also, what would be the way to solve this proof then?
Click here to see answer by jim_thompson5910(35256)

Question 1102118: I�m doing homework concerning the rules of replacement. We are allowed to use 8 rules of implication (modus ponens, modus tollens, pure hypothetical syllogism, disjunctive syllogism, constructive dilemma, simplification, conjunction, and addition) and 10 rules of replacement (De Morgan�s rule, commutativity, associativity, distribution, double negation, transposition, material implication, material equivalence, exportation, and tautology). I have been stuck on the same proof for several days, trying different solutions for multiple hours each day. The problem is as follows:
Premise 1: If Q, then (A and V)
Premise 2: If (If not V, then C), then B
Conclusion: If Q, then B
Even a nudge in the right direction would be appreciated. Thank you.
Click here to see answer by jim_thompson5910(35256)

Question 1104281: Use Mathematical Induction to show that the following statement is true for all natural numbers n:

Click here to see answer by stanbon(75887)

Question 1104281: Use Mathematical Induction to show that the following statement is true for all natural numbers n:

Click here to see answer by math_helper(2461)

Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485