Tutors Answer Your Questions about Proofs (FREE)
Question 1066422: write a direct proof using the eight rules of inference
(C → Q) (~L → ~R), (S → C) (~N → ~L), ~Q J, ~Q → (S v ~N), therefore, ~R
i have to use the eight rules, but this particular problem is very hard for me. hoping you can help.
this is from the power of logic 5th edition.
these are the rules im being given.
Rule 1: Modus ponens (MP): p → q
p
∴ q
Rule 2: Modus tollens (MT): p → q
∼q
∴ ∼q
Rule 3: Hypothetical syllogism (HS): p → q
q → r
∴ p → r
Rule 4: Disjunctive syllogism (DS), in two forms:
p ∨ q p ∨ q
∼p ∼q
∴ q ∴ p
Rule 5: Constructive dilemma (CD): p ∨ q
p → r
q → s
∴ r ∨ s
Rule 6: Simplification (Simp), in two forms:
p q p q
∴ p ∴ q
Rule 7: Conjunction (Conj): p
q
∴ p q
Rule 8: Addition (Add) in two forms:
p p
∴ p ∨ q ∴ q ∨ p
Click here to see answer by Edwin McCravy(20054)   |
Question 1067206: Hello team, would you be so kind to assist with this problem below. Ive tried to figure out but was wrong. some help is greatly appreciated!
use one of the indirect proof techniques (reduction ad absurdum or conditional proof RAA) to demonstrate the validity of the argument -
(G P) → K, E → Z, ~P → ~ Z, G → (E v L), therefore, (G ~L) → K
Click here to see answer by Edwin McCravy(20054)   |
Question 1070285: Prove that for any integer n, 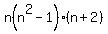 is divisible by 12. is divisible by 12.
Below is my attempt at trying to solve it, however I don't think example is enough to show as proof.
we want to prove 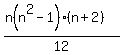 . I written it also as . I written it also as
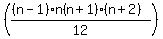 which if you plug in 2 or 3 it will give an even number in the numerator which means it can be divisible by 12. which if you plug in 2 or 3 it will give an even number in the numerator which means it can be divisible by 12.
Click here to see answer by ikleyn(52778)   |
Question 1074058: let X IS NOT EQUAL TO 0.let X approach to X be a bijective mapping, define
F=(A subset of X : A=f^-1(B) for some B subset of X)
is F a sigma-algebra over X? if so prove. if not,state and show that which property is not satisfied.
Click here to see answer by ikleyn(52778)   |
Question 1074715: Prove or disprove the statements below.
(a) For all positive real numbers x and y, ⌊x*y⌋ ≤ ⌊x⌋*⌊y⌋
(b) For all positive real numbers x and y, ⌈x*y⌉ ≤ ⌈x⌉*⌈y⌉
I am not sure where to start, could someone please give me some hints on how to solve these kind of question. Thank you in advance.
Click here to see answer by Edwin McCravy(20054)   |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485
|


