Question 9013: How can you prove that:
odd + odd = even
even + even = even (you initially put even + even = odd)
odd + even = odd
????
Answer by prince_abubu(198)   (Show Source):
You can put this solution on YOUR website! We're going to do some backwards thinking here. Hang on.
We all know that a number that ends in 0,2,4,6, or 8 is even. OK. Take ANY integer n, and you can even pick an odd number if you want. Multiply it by 2. That number n times 2 will ALWAYS turn out even. You can't help it. Now, think of it backwards: If a number A is even, it must be able to be expressed as 2*n. If A is even, then there is an integer n such that  . You can think of this trick as forcing a given variable to be even.
What about forcing a variable to be odd? Let's do this forwards first. We know that if you take any integer n and multiply it by 2, the product 2*n is ALWAYS even. Add one to that product and you will ALWAYS end up with an odd result. In other words, the quantity  is ALWAYS odd. Thinking of it backwards, you can force the number B to be odd by declaring  . AKA, there is such a number n such that the quantity is always undoubtedly ODD.
---------------------------------------------------------
Now, let's try to prove that ODD + ODD = EVEN. Let's choose two odd variables C and D. If C is odd, then C must be expressed as , where n is any integer. If D is odd, then D must be expressed as 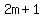 . Notice that we used two different variables n and m. This shows us that C and D don't have to be the same number, just as long as they're both odd. Now, let's plug it in to our equation:
(2n + 1) + (2m + 1) ?= even? <---- START
2n + 2m + 2 ?= even? <------ START No matter what n and m are, 2n and 2m will ALWAYS be even. and the 2? 2 is even, so adding an even to an even creates an even number.
odd + odd = even <----- final answer
------------------------------------------------------------------
If you've got two even numbers to add up, the answer is always even. Let's choose two numbers, E and F. If E and F are indeed even, then there must be integers p and q so that we can say that  and 
So let's put these to the test: 2p + 2q ?= even?
2(p + q) ?= even? <------------- Factor out the 2 from both terms. It seems like it doesn't matter what p and q are. Their sum will be multiplied by 2, forcing the answer to be even.
--------------------------------------------------------------------
What about odd + even = odd? Let's choose G and H as the odd and even numbers to be added. If G is odd, then it can be written as G = 2r + 1 and r is any integer. If H is even, then it can be written as H = 2s and s is ANY integer. Let's test this:
(2r + 1) + 2s ?= odd <----------------- start
2r + 2s + 1 ?= odd <---------------- rearrange
2(r + s) + 1 ?= odd <-------------- factor out the 2 from the 2r and 2s. No matter what r and s are, their sum will be multiplied by 2, forcing an even number answer. Then you've got the + 1 that forces the already even answer to be odd.
|
|
|
