SOLUTION: The question is as under : " Alight house is located at A, 2 km off-shore from the nearest point O on a straight beach and a shop is located at B. The shop is located on the beach

Algebra ->  Proofs -> SOLUTION: The question is as under : " Alight house is located at A, 2 km off-shore from the nearest point O on a straight beach and a shop is located at B. The shop is located on the beach      Log On


   

Question 890509: The question is as under :
" Alight house is located at A, 2 km off-shore from the nearest point O on a straight beach and a shop is located at B. The shop is located on the beach , 4 km distant from O. If the housekeeper can row at the rate of 4 km/hour and walk at the rate of 6 km/hr, where should he plan to reach the shore, so as to cover the distance to the shop in the least possible time ? "
The question is related to maxima and minima chapter in differential calculus.
Please send step by step solution of the above question.
Regards,
Khoka123
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
A light house, a shop, and a housekeeper. Where does the housekeeper begin? From the light house? I could analyze and solve the problem if you make the description understandably precise.

---
I believe I have an understanding of the description after thinking through the description.

Draw a right triangle. Vertical segment OB, showing B below O, and point A to the right of point O. Segment OB is 4, and segment OA is 2. The angle AOB is a right angle.

The housekeeper will row from the light house (?) to point P between O and B.

Let y = Distance for walking which is segment PB.
That means 4-y is length of OP.

Distance Rowing, 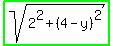highlight_green%28sqrt%282%5E2%2B%284-y%29%5E2%29%29
Distance Walking, highlight_green%28y%29.

Uniform Rates usually for travel can be represented RT=D, or T=D/R.
Using a function for total time, T you have total time for this housekeepers row & walk trip as highlight_green%28T=sqrt%284%2B%284-y%29%5E2%29%2F4%2By%2F6%29.

Find the derivative, 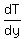dT%2Fdy.
In one of its raw forms, this starts as:



---
Equating that to 0, and then omitting the many algebra steps here, I am finding highlight%2813y%5E2%2B40y%2B192=0%29; if this has a real solution, then I believe I made no mistakes...

I MADE A MISTAKE IN MY WORK, SOMEWHERE. MAYBE YOU WILL FIND IT AND GET THE RIGHT ANSWER.


RETRIED SOLUTION-------------------------------------------------------
The same formula for T was found.
Derivative dT%2Fdy=-%28%284-y%29%2F%28sqrt%284%2B%284-y%29%5E2%29%29%29%2B1%2F6.
Simplifying and then focusing on the numerator being 0 gave highlight%2835y%5E2-280y%2B4=0%29.
Two solutions for y were found, and the choice which makes sense was highlight%28y=0.18%29.
The calculations and computation to find that are omitted here, taking nearly a whole page on paper.

The housekeeper would row to a point between O and B, 0.18 km from the point B (the shop).