Question 1207211: Can you please help me solve the following trigonometry exact values with working out:
sin 2pi/3
cos 3pi/4
tan 5pi/6
sin 7pi/6
cos 5pi/4
tan 4pi/3
sin 5pi/3
cos 7pi/4
tan 11pi/6
I know it is a lot of questions to ask but I am quite stuck. It would be nice if all of them are complete but if this is too much to ask for atleast half to 3/4s of them would be nice. Thankyou!
Found 2 solutions by Theo, math_tutor2020:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! it is easiest to convert the radians to degrees and work from that.
it is also easiest to work from reference angles as well.
it is useful to use the calculator to confirm that you are correct.
there's a table of trig values for common angles that can help you.
it is at https://www.mathematicalway.com/mathematics/trigonometry/trigonometric-ratios/
this is what the one we will be using look like.
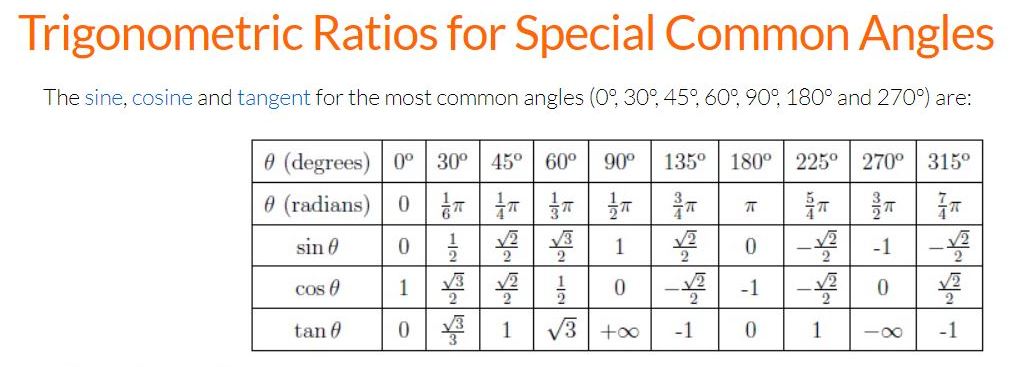
here are the rules for determining the reference angle.
the reference angle is the equivalent angle in the first quadrant.
if the angle is in the first quadrant, the reference angle is equal to that angle.
if the angle is in the second quadrant, the reference angle is equal to 180 minus that angle.
if the angle is in the third quadrant, the reference angle is equal to that angle minus 180 degrees.
if the angle is in the fourth quadrant, the reference angle is equal to 360 minus that angle.
rule for trig signs are as follows:
sine is positive in the first and second quadrant, negative in the third and fourth quadrant.
cosine is positive in the first and fourth quadrant, negative in the second and third quadrant.
tangent is positive in the first and third quadrant, negative in the second and fourth quadrant.
first is sin(2pi/3).
multiply by 180/pi to get 2pi/3*180/pi = 2*180/3 = 120 degrees.
that angle is in the second quadrant.
reference angle is 180 - 120 = 60 degrees.
sine of 60 degrees is sqrt(3)/2.
sine is positive in the first and second quadrants, so sine of 120 is also equal to sqrt(3)/2.
to confirm, set your calculator to radians and find sin(2pi/3).
you will get 2.094395102
enter 2 * sqrt(3) / 2 in your calculator.
it will be equal to the same, confirming you are correct.
second is cos(3pi/4).
multiply by 180/pi to get 3pi/4 * 180/pi = 3*180/4 = 135 degrees.
that angle is in the second quadrant.
equivalent angle in the first quadrant is 180 - 135 = 45 degrees.
cosine of 45 degrees is equal to sqrt(2)/2.
cosine is negative in the second quadrant, so cosine(135) degrees is -sqrt(2)/2.
to confirm, set your calculator to radians and find cosine 135 degrees.
you will get -.7071067812
enter -sqrt(2)/2 in your calculator.
you will get the same, confirming you are correct.
third is tan (5pi/6).
multiply by 180/pi to get 5pi/6 * 180/pi = 150 degrees.
that angle is in the second quadrant.
reference angle is 180 minus 150 = 30 degrees.
tan(30) = sqrt(3)/3.
tangent is positive is negative in the second quadrant.
tan(150) is equal to -sqrt(3)/3.
set your calculator to radians.
tan(5pi/6) = -.5773502692
-sqrt(3)/3 = the same, confirming you are correct.
next is sin (7pi/6).
multiply by 180/pi to get 7pi/6 * 180/pi = 210 degrees.
210 degrees is in the third quadrant.
reference angle is 210 minus 180 = 30 degrees.
sine of 30 degrees is equal to 1/2.
sine is negative in the third quadrant
sine of 210 degrees is equal to -1/2.
to confirm, set your calculator to radians if is not already set to that.
-1/2 = -.5
sin(7pi/6) = the same, confirming you are correct.
next is cos(5pi/4).
multiply by 180/pi to get 5pi/4 * 180/pi = 5*180/4 = 225 degrees.
225 is in the third quadrant.
reference angle is 225 minus 180 = 45 degrees.
cosine 45 degrees is sqrt(2)/2.
cosine is negative in the third quadrant.
cos(5pi/4) is equal to -sqrt(2)/2.
confirm by using your calculator.
-sqrt(2)/2 = -.7071067812.
cos(5pi/4) = the same, confirming you are correct.
next is tan(4pi/3).
multiply by 180/pi to get 4pi/3 * 180/p = 4*180/3 = 240.
240 is in the third quadrant.
reference angle is 240 minus 180 = 60 degrees.
tangent 60 degrees is equal to sqrt(3).
tangent is positive in the third quqadrant.
tan(4pi/3) = sqrt(3).
use your calculator to confirm.
sqrt(3) = 1.732050808.
tan(4pi/3) = the same, confirming you are correct.
next is sin(5pi/3).
multiply by 180/pi to get 5pi/3 * 180/pi = 4*180/3 = 300.
that angle is in the fourth quadrant.
reference angle is 360 minus 300 = 60 degrees.
sine of 60 degrees is sqrt(3)/2.
since is negative in the fourth quadrant.
sin(5pi/3) = -sqrt(3)/2.
use your calculator to confirm.
-sqrt(3)/2 = -.8660251038.
sin(5pi/3) = the same, fonriming your are correct.
next is cos(7pi/4).
multiply by 180/pi to get 7pi/4 * 180/pi = 7*180/4 = 315 degrees.
315 degrees is in the fourth quadrant.
reference angle is 360 minus 315 = 45 degrees.
cosine(45) degrees is sqrt(2)/2.
cosine is positive in the fourth quadrant.
cos(7pi/4) = sqrt(2)/2.
confirm using your calculator.
sqrt(2)/2 = .7071067812.
cos(7pi/4) = the same, fonriming you are correct.
last is tan(11pi/6).
multiply by 180/pi to get 11pi/6 * 180/pi = 11*180/6 = 330 degrees.
330 is in the fourth quadrant.
reference angle id 360 minus 330 = 30 degrees.
tan(30) = sqrt(3)/3.
tangent is negative in the fourth quadrant.
tan(11pi/6) = -sqrt(3)/3.
confirm using your calculator.
-sqrt(3)/3 = -.5773502692.
tan(11pi/6) = the same, confirming you are correct.
that should do it.
since the table also shows the angle in radians, you could also have just stayed with radians.
you still needed to get the reference angle.
the rules for finding the reference angle in radians would be.
if the angle is between 0 and pi(same as between 0 and 90), it's in the first quadrant and the reference angle is equal to the angle.
if the angle is between pi and 2pi (same as between 90 and 180), it's in the second quadrant and the reference angle is equal to 2pi minus the angle.
if the angle is between 2pi and 3pi/2 (same as between 180 and 270), it's in the third quadrant and the reference angle is equal to that angle minus 2pi.
if the angle is between 3pi/2 and 2pi (same as between 270 and 360), it's in the fourth quadrant and the reference angle is equal to 2pi minus the angle.
i'll use last problem to show you how it works.
you are looking for tan(11pi/6).
270 degrees * pi/180 = 270/180 * pi = 3/2 * pi.
3/2 * pi = 9/6 * pi
11pi/6 is greater than 9/6 * pi.
2pi = 12pi/6 is greater than 11pi/6.
11pi/6 is in the fourth quadrant.
11pi/6 is in the fourth quadrant.
the reference angle is 2pi minus 11pi/6 = 12pi/6 minus 11pi/6 = pi/6.
from the table, tan(pi/6) = sqrt(3)/3.
you get to the same place, but it's a little harder to figure it out, which is why i recommend converting to degrees first.
let me know if you have any questions.
theo
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If you are allowed access to the Unit Circle then it's best to use it

Image Source:
https://www.mathsisfun.com/geometry/unit-circle.html
The x and y coordinates of the terminal point represent the cosine and sine values respectively.
For example,
cos(pi/3) = 1/2
sin(pi/3) = sqrt(3)/2
pi/3 radians = 60 degrees
Focus on the upper right corner known as quadrant I.
Notice 30-60-90 triangles are useful for the 30 and 60 degree angles.
A 45-45-90 triangle is useful for the 45 degree angle.
Use the appropriate template for each.
Once you've memorized the items in the 1st quadrant, you can then use symmetry to apply things to the other quadrants.
One last thing to note:
tangent is the ratio sine/cosine
So to compute something like tan(11pi/6), you'll divide the values sin(11pi/6) over cos(11pi/6).
--------------------------------------------------------------------------
With all that in mind you should get these answers
sin(2pi/3) = sqrt(3)/2
cos(3pi/4) = -sqrt(2)/2
tan(5pi/6) = -sqrt(3)/3
sin(7pi/6) = -1/2
cos(5pi/4) = -sqrt(2)/2
tan(4pi/3) = sqrt(3)
sin(5pi/3) = -sqrt(3)/2
cos(7pi/4) = sqrt(2)/2
tan(11pi/6) = -sqrt(3)/3
Please let me know if you have a specific question about how to arrive at any one of these answers.
One way to verify the answers is to use WolframAlpha. GeoGebra is another useful option (you'll need to use the CAS tool). There are many other ways to verify.
|
|
|