Question 947653: the digits of a three digit natural number are in A.p and their sum is 18.the number obtained by reversing the digits is 594 less than the original number.find the original number.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! WITHOUT ALGEBRA:
The average of  consecutive terms (or any odd number of terms) of an A.P. (arithmetic progression, or arithmetic sequence, depending on where you live) is equal to the middle term. consecutive terms (or any odd number of terms) of an A.P. (arithmetic progression, or arithmetic sequence, depending on where you live) is equal to the middle term.
So, the middle digit is  . .
Since reversing the digits makes a lesser number (594 less than the original number),
the digits decrease from left to right.
(They do not stay the same or increase).
The first digit, being greater than  , ,
could be  , ,  , or , or  . .
If the first digit were  , the last digit would be , the last digit would be  , ,
and the 3-digit number would be 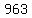 . .
Then, reversing the digits we would get 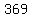 , ,
and the difference would be  . .
If the first digit were  , the last digit would be , the last digit would be  . .
If the first digit were  , the last digit would be , the last digit would be  . .
In either case the difference between the number obtained by reversing the digits and the original number would be less than 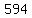 . .
Som the original number is  . There is no other choice. . There is no other choice.
USING ALGEBRA TO MAKE IT MORE COMPLICATED:
Let  be the first digit and be the first digit and  be the common difference. be the common difference.
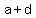 = the second digit, and = the second digit, and
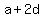 = the third digit. = the third digit.
so, "their sum is 18" translates as
 --> -->  --> -->  ---> --->  . .
The value of the number obtained by reversing the digits is
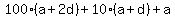 . .
Since the value of the number obtained by reversing the digits is 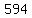 less than the value of the original number, less than the value of the original number,

Simplifying







Substituting that value into the other equation,  , ,
we get  --> -->  --> -->  --> -->  , ,
and having the second digit,  , ,
the first digit,  , and the common difference , and the common difference  , ,
we can find the third digit,
 , ,
and then we know that the original number was  . .
|
|
|