Question 934070: A toy rocket is launched from the ground level with an initial velocity of 96ft/s. After how many seconds will the rocket hit the ground?
In this problem, I understand that I have to make a parabola. This means that the 96ft/s will be the peak of the parabola and the x axis should mark the start and end point (when it hits the ground). However, I don't know how to make the algebraic expression that goes with it. If I can make the algebraic expression, I know that I have to use (-1)b/2a to find the x intercept, and then plug that number in to find the other x intercept.
Please help...
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! To solve the problem, you need a little more knowledge of physics.
On or near the surface of planet Earth,
anything not being held/pushed up falls down
(towards the center of the Earth) with an acceleration of about  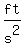 . .
Toy rockets get a very short push, to get an initial speed,
and then they are not being pushed up any more.
The upwards velocity of the rocket will decrease by  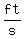 every second. every second.
The graph of upwards velocity as a function of time looks like this

The upwards velocity starts a s 96 ft/s at time zero,
is zero at 3 seconds, and is negative (rocket falling down) after 3 seconds.
It takes 3 seconds  for the rocket to get to the highest point, for the rocket to get to the highest point,
and another 3 seconds for it to return to the height where it started
(disregarding air resistance, of course),
so the total flight time is  seconds. seconds.
A math teacher will have told you that on Earth
the height (in feet) as function of time since launch (in seconds)
of a projectile launched upwards with an initial speed  ft/s ft/s
from an initial height  feet is feet is
 . .
The teacher will have told you that the graph of that equation is a parabola,
and wouldn't you like to believe and memorize that equation?
Using that equation, with  and and  you get you get
 , and the rocket is on the ground when , and the rocket is on the ground when  , ,
which will happen for the solutions to
 <---> <--->  ---> --->  . .
A physics teacher may tell you that you need to know calculus to derive that equation.
I would tell you that it comes very naturally from the graph.
Since upwards velocity multiplied times seconds in flight equals gain in height,
the gain in height is the area above the x-axis
and below the graph of upwards velocity as a function of time.
For a real rocket that could maintain the constant velocity  , ,
the graph would be a flat line, and
the gain in height as a function of time would be
 , ,
the area of a rectangle under the flat line:

In the case of the toy rocket, the graph is a straight line sloping down,
so you have to subtract a right triangle from that rectangle.
The triangle to be subtracted has legs measuring  and and 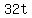 , ,
so its area is  : :
 so the change in height is the area of the trapezoid with green and red sides: so the change in height is the area of the trapezoid with green and red sides:
 . .
|
|
|