Question 922257: sum of 6 consecutive even numbers is 618.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! MENTAL MATH (if you just need a quick answer):
The number in the middle of those 6 consecutive even numbers is  . (It is the average and the median of the 6 consecutive even numbers, because they form an arithmetic sequence. If you learned about arithmetic sequences, you may have been taught that). . (It is the average and the median of the 6 consecutive even numbers, because they form an arithmetic sequence. If you learned about arithmetic sequences, you may have been taught that).
The 6 consecutive even numbers are
 , ,  , ,  , ,  , ,  , and , and  . .
SHOWING YOUR WORK (with lots of explanations):
First, you define a variable in the most convenient way you can think of.
You do not need to call one of your even numbers 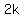 with with  = an integer to show that it is an even number. = an integer to show that it is an even number.
You can call one of those 6 even numbers  , and when you solve for , and when you solve for  , check if it is an even number. If the , check if it is an even number. If the  you find is not even, there is no solution. you find is not even, there is no solution.
One option is  = the smallest of the 6 consecutive even numbers. = the smallest of the 6 consecutive even numbers.
If you learned about arithmetic sequences, you can try to use some formulas from that, but it may be more trouble than it's worth.
If the smallest even integer is  , the other 5 even numbers are , the other 5 even numbers are  , , 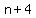 , , 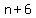 , , 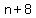 , and , and 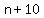 . .
The sum is

 ---> ---> ---> ---> ---> ---> ---> --->
Another option would be saying that the 6 consecutive even numbers are
 , ,  , ,  , ,  , ,  , and , and  . .
The difference between one and the next is 2, so they are either 6 consecutive even numbers, or 6 consecutive odd numbers.
Their sum is

 ---> ---> ---> ---> ---> ---> . .
|
|
|