Question 856303: Find two consecutive integers such that three Times the square if the first integer plus three is equal to 5 times the second integer.
Can someone explain how to solve this please.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, you set up an equation and solve it.
Then, you discard any solution that does not fit the description.
(In this case the description is "integer",
but some problems refer to "even integer", or "odd integer").
You need to define your "two consecutive integers".
You may write  = the first integer, = the first integer,
to define your variable.
Or you could also use  for your variable. for your variable.
Using  , you know (and may, or may not want to write) that: , you know (and may, or may not want to write) that:
 = the second integer = the second integer
 = the square of the first integer, = the square of the first integer,
 = three times the square of the first integer, = three times the square of the first integer,
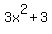 = three times the square of the first integer plus three, and = three times the square of the first integer plus three, and
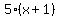 = 5 times the second integer = 5 times the second integer
Your equation is

Then you work on rearranging and simplifying your equation as needed:




Finally, you solve by a method of your choice.
In this case, I would use the quadratic formula,
which says that the solutions to
 are given by are given by
 . .
In this case, applying the quadratic formula, we get




You get the solutions
 --> --> --> -->
and  --> --> --> -->
Since  is not an integer, it is not a solution to the problem, and you discard it. is not an integer, it is not a solution to the problem, and you discard it.
The two consecutive integers are  and and  . .
Verification:
 would be three times the square of the first integer plus three; would be three times the square of the first integer plus three;
 would be "5 times the second integer", would be "5 times the second integer",
and both quantities are equal, as the problem required.
|
|
|