Question 845227: The product of two positive consecutive odd integers is 1 less than 5 times their sum.
Find the integers
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 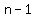 = the smallest of the two consecutive odd integers. = the smallest of the two consecutive odd integers.
 = the next odd integer (the other one of the two consecutive odd integers). = the next odd integer (the other one of the two consecutive odd integers).
 = the sum of the two consecutive odd integers. = the sum of the two consecutive odd integers.
 = the product of the two consecutive odd integers. = the product of the two consecutive odd integers.
The equation is

Solving:



Since 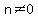 , I can divide both sides by , I can divide both sides by  and get and get


So  --> -->  , and , and
 --> --> 
Verification:
The numbers  and and  are odd. are odd.
Their sum is  . .
Five times their sum is  . .
One less than 5 times their sum is  . .
Their product is  and that is exactly "1 less than 5 times their sum." and that is exactly "1 less than 5 times their sum."
NOTES:
I could have called the two consecutive odd integers  and and  , ,
but I thought that would make the calculations more complicated.
Someone could think to call the two odd integers 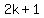 and and 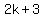 , ,
or 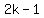 and and 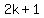 , ,
but that was going to make it more complicated.
If there are consecutive odd integers, or consecutive even integers,
just call them  and and 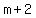 , ,
or 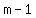 and and 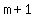 . .
Those expressions do not say that the numbers are even or odd,
but they say that they are the same kind (both odd or both even),
and when you find the solution you can verify if it is the right kind.
|
|
|