SOLUTION: Use polynomial long division to divide 4x3 + x2 + 17x – 15 by -x2 – x – 5 can someone walk me through this

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: Use polynomial long division to divide 4x3 + x2 + 17x – 15 by -x2 – x – 5 can someone walk me through this      Log On


   

Question 512996: Use polynomial long division to divide
4x3 + x2 + 17x – 15
by
-x2 – x – 5
can someone walk me through this
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
           ____________________ 
-x² – x – 5)4x³ + x² + 17x – 15


We divide the 4x³ by -x²:  %284x%5E3%29%2F%28-x%5E2%29 = -4x, so we put that
above the 17x like this:

                       -4x        
-x² – x – 5)4x³ + x² + 17x – 15


Then we multiply -4x by -x² - x - 5:  -4x(-x² - x - 5) = 4x³ + 4x² + 20x
and write that down below 

                        -4x       
-x² – x – 5)4x³ +  x² + 17x – 15
            4x³ + 4x² + 20x

Next we draw a line under that 

                        -4x     
-x² – x – 5)4x³ +  x² + 17x – 15
            4x³ + 4x² + 20x

Now we subtract, imagining all the signs changed like this
and adding:                
                                4x³ +  x² + 17x 
                               -4x³ - 4x² - 20x
                                     -3x² -  3x 

We write that down under the line:

                       -4x                                
-x² – x – 5)4x³ +  x² + 17x – 15
            4x³ + 4x² + 20x
                 -3x² -  3x

We bring down the -15

                       -4x       
-x² – x – 5)4x³ +  x² + 17x – 15
            4x³ + 4x² + 20x
                 -3x² -  3x - 15

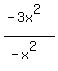We divide the -3x² by -x²:  %28-3x%5E2%29%2F%28-x%5E2%29 = +3, so we put that
above the -15 like this (don't forget the + sign:
        
                       -4x  +  3 
-x² – x – 5)4x³ +  x² + 17x – 15
            4x³ + 4x² + 20x
                 -3x² -  3x - 15
 
Then we multiply +3 by -x² - x - 5:  +3(-x²-x-5) = -3x² - 3x - 15
and write that down below


                       -4x  +  3  
-x² – x – 5)4x³ +  x² + 17x – 15
            4x³ + 4x² + 20x
                 -3x² -  3x - 15
                 -3x² -  3x - 15


Next we draw a line under that 

                       -4x  +  3  
-x² – x – 5)4x³ +  x² + 17x – 15
            4x³ + 4x² + 20x
                 -3x² -  3x - 15
                 -3x² -  3x - 15


Now we subtract, imagining all the signs changed like this
and adding:                
                               -3x² -  3x - 15 
                                3x² +  3x + 15
                                             0

And we get a 0 remainder, so the answer is the quotient -4x + 3

Edwin