Question 242519: the largest 3 consecutive integers for which the first is increased by twice the second exceeds the third by less than 25. (have to solve algrebraically)
I do not know how to put "exceeds" in an equation.
Please give me the answer and a detailed explanation of it!
Found 2 solutions by ankor@dixie-net.com, MathTherapy:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Three consecutive integers, x, (x+1), (x+2);
:
the largest 3 consecutive integers for which the first is increased by twice the second exceeds the third by less than 25.
:
Exeeds by less than 25 so try 24,
:
x + 2(x+1) = (x+2) + 24
x + 2x + 2 = x + 26
x + 2x - x = 26 - 2
2x = 24
x = 12
:
12, 13, 14 are the integers
:
See if that is true in the given statement
first is increased by twice the second exceeds the third by less than 25.
12 + 2(13) = 14 + 24
12 + 26 = 38
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website! the largest 3 consecutive integers for which the first is increased by twice the second exceeds the third by less than 25. (have to solve algrebraically)
I do not know how to put "exceeds" in an equation.
Let the 1st of the 3 consecutive integer be F
Then the 2nd and 3rd integers are F + 1, and F + 2, respectively
Increasing the 1st by twice the second gives us F + 2(F + 1). Since this result exceeds the third by less than 25, it means that F + 2(F + 1) is greater than the 3rd integer, and when the 3rd integer, or F + 2 is subtracted from F + 2(F + 1), we should get a number that is less than 25. Therefore, putting this in mathematical terminology, we get:
F + 2(F + 1) - (F + 2) < 25
F + 2F + 2 - F - 2 < 25
2F < 25
Therefore, F, or the 1st number < 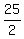 , or < 12.5 , or < 12.5
Since we're talking about INTEGERS, then the integer that is less than 12.5 is 12. Therefore, with F, or the 1st integer being 12, the 3 INTEGERS are  . .
|
|
|