Question 207613: 3 consecutive even numbers where the product of the smaller two numbers is 52 less than the square of the largest number.
Found 2 solutions by checkley77, MathTherapy:
Answer by checkley77(12844)   (Show Source):
You can put this solution on YOUR website! Let x, x+1 & x+2 be the three numbers.
x(x+1)+52=(x+2)^2
x^2+x+52=x^2+4x+4
x^2-x^2-4x+x=4-52
-3x=-48
x=-48/-3
x=16 ans. for the smallest number
16=1=17 ans. for the middle number
16+2=18 ans. for the largest number
Proof
16*17+52=18^2
272+52=324
324=324
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
3 consecutive even numbers where the product of the smaller two numbers is 52 less than the square of the largest number.
Let the smallest number be S
Then the other two numbers, since these are EVEN numbers are: S + 2, and S + 4
Now, since the product of the smaller two numbers is 52 less than the square of the largest number, we have:
2S - 8S = 16 - 52
- 6S = - 36
 = 6
Therefore, the smallest number is  , the second smallest is  (6 + 2), and the largest is  (6 + 4)
-----------
Check:
------------
The product of the two smaller numbers, 6 and 8 is 48 (6 * 8)
The square of the largest number, 10, is 100 ( )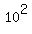
48 (the product of the two smaller numbers) is 52 less than 100 (the square of the largest number)
PLUS, the THREE are CONSECUTIVE EVEN NUMBERS
|
|
|
